26-06-2025 - Exercise - Study of two functions [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH

26-06-2025 - Exercise - Study of two functions [EN]-[IT]
In this post I would like to propose an exercise, both to understand some concepts and to develop a little logical and analytical thinking.
This exercise is based on mathematical analysis
(code notes: X-89)

START
Exercise 01
Considering the following function

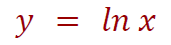
Which of these considerations is correct?
1-passes through the point (0,1) and is unlimited
2-passes through (1,0) and is increasing and unlimited
3-passes through the point (0,1) and is positive and increasing
2-passes through (1,0) and is positive
Development
First of all we must identify the writing ln x. This is the natural logarithm of x.
The natural logarithm is the logarithm to the base e.
Where: e ≈ 2.71828
We can say that

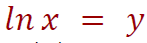
is equivalent to

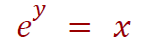
Now let's start examining the function, here are the considerations to make.
-The domain is x > 0
-The intersection with the x-axis occurs at ln 1 = 0, so it passes through the point (1,0)
-The function is increasing throughout its domain, so it is to be considered increasing -The function tends to -∞ for x --> 0+ and to +∞ for x --> +∞, so we can say that it is unlimited -It is positive only for x >1 and negative for 0 < x < 1, so we know its sign. 1

Below is the graph of the function

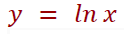
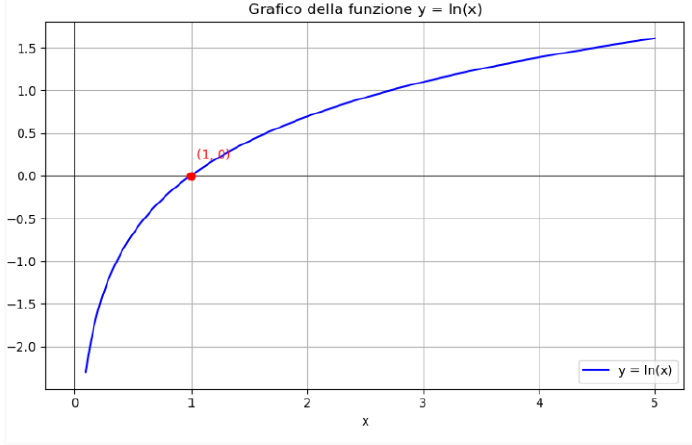
image created with artificial intelligence, the software used is Microsoft Copilot

Answer Going to analyze the options, we can now say that the second one is the correct one. So this function passes through (1,0), is increasing and unbounded

Exercise 02
What is the domain of the following function?

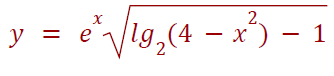
Initial analysis
The domain and the codomain can be considered as two main concepts of functions.
The domain is the set of all input values ​​for which the function is defined, i.e. x.
The codomain is the set of all possible output values, i.e. y.
We can say that the domain is the set of values ​​that can be inserted into a function, while the codomain is the set of results of the function.
Development
First we must consider that the exponential function e^x is defined for every x that belongs to R (for every x that belongs to the set of real numbers, that is, integers, rational numbers, irrational numbers, positive numbers, negative numbers and zero). The part under the root must be ≥ 0 so we can develop that part and arrive at the inequality

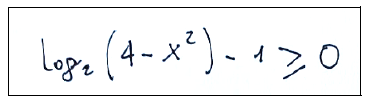
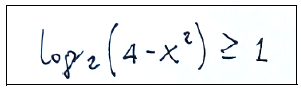
We can now solve the inequality

and now we can identify the domain

Answer
So the correct answer is that the domain is the next

That is, x is a real number between -√2 and √2, inclusive.

Conclusions
The study of functions is important to understand how one variable depends on another, functions are like a sort of model of relationships between quantities. For example, we can study temperature as a function of time or we can relate the cost of a product as a function of quantities.
Function studies also help to make decisions.

Question
A logarithmic function (like the one seen in this exercise) is practically the inverse of the exponential. Did you know that if a quantity grows exponentially, the logarithm is used to calculate the time required to reach a certain value?

---

---

ITALIAN

26-06-2025 - Exercise - Studio di due funzioni [EN]-[IT]
In questo post vorrei proporre un esercizio, sia per comprendere alcuni concetti sia per sviluppare un poco il pensiero logico e analitico.
Questo esercizio si basa sull’analisi matematica
(code notes: X-89)

START
Esercizio 01
Prendendo in considerazione la seguente funzione

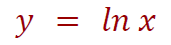
Quale di queste considerazioni è corretta?
1-passa per il punto (0,1) ed è illimitata
2-passa per (1,0) ed è crescente e illimitata
3-passa per il punto (0,1) ed è positiva e crescente
2-passa per (1,0) ed è positiva
Sviluppo
Innanzi tutto dobbiamo identificare la scritta ln x. Questo è il logaritmo naturale di x.
Il logaritmo naturale è il logaritmo in base e.
Dove: e ≈ 2,71828
Possiamo dire che

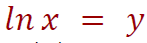
equivale a

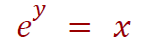
Ora iniziamo con esaminare la funzione, qui di seguito le considerazioni da fare.
-Il dominio è x > 0
-L’intersezione con l’asse x avviene in ln 1 = 0, quindi passa per il punto (1,0)
-La funzione è crescente per tutto il suo dominio, quindi è da ritenersi crescente -La funzione tende a -∞ per x --> 0+ e a +∞ per x --> +∞, quindi possiamo dire che è illimitata -è positiva solo per x >1 e negativa per 0 < x < 1, quindi ne conosciamo il segno. 1

Qui di seguito il grafico della funzione

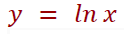
immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Risposta Andando ad analizzare le opzioni, possiamo ora dire che la seconda è quella corretta. Quindi questa funzione passa per (1,0), è crescente e illimitata

Esercizio 02
Qual è il dominio della seguente funzione?

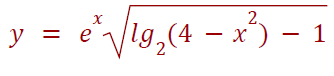
Analisi iniziale
Possono essere considerati come due concetti principali delle funzioni il dominio ed il codominio.
Il dominio è l’insieme di tutti i valori di ingresso per cui la funzione è definita, cioè la x.
Il codominio è l’insieme di tutti i valori possibili di uscita, cioè la y.
Possiamo dire che il dominio è l’insieme dei valori che si possono inserire in una funzione, mentre il codominio è l’insieme dei risultati della funzione.
Sviluppo
Per prima cosa dobbiamo considerare che la funzione esponenziale e^x è definita per ogni x che appartiene ad R (per ogni x che appartiene all’insieme dei numeri reali, cioè numeri interi, razionali, irrazionali, positivi, negativi e zero) La parte sotto radice deve essere ≥ 0 quindi possiamo sviluppare quella parte ed arrivare alla disuguaglianza

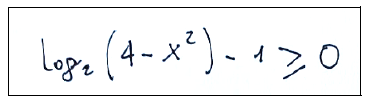
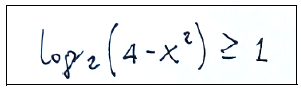
Possiamo ora risolvere la disuguaglianza

ed ora possiamo identificare il dominio

Risposta
Quindi la risposta corretta è che il dominio è il seguente

Cioè x è un numero reale compreso tra -√2 e √2, inclusi.

Conclusioni
Lo studio delle funzioni è importante per capire come una variabile dipende da un'altra, le funzioni sono come una sorta di modello di relazione tra grandezze. Ad esempio possiamo studiare la temperatura in funzione del tempo oppure possiamo mettere in relazione il costo di un prodotto in funzione delle quantità.
Gli studi di funzione aiutano anche a prendere delle decisioni.

Domanda
Una funzione logaritmica (tipo quella vista in questo esercizio) è praticamente l'inversa dell'esponenziale. Lo sapevate che se una grandezza cresce esponenzialmente, il logaritmo serve a calcolare il tempo necessario per raggiungere un certo valore?

THE END