10-04-2025 - Physics - Conservation of mechanical energy [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH

10-04-2025 - Physics - Conservation of mechanical energy [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_81-80)

Conservation of mechanical energy

image created with artificial intelligence, the software used is Microsoft Copilot

Introduction
What is the conservation of mechanical energy?
The conservation of mechanical energy is an important principle of physics. This principle states that, in a closed system and in the absence of dissipative forces, such as friction, the total mechanical energy remains constant over time.
Mathematically it can be expressed as follows:

Where:
Em = total mechanical energy
Ec = kinetic energy
Ep = potential energy

Kinetic energy and potential energy
In the formula expressed before, kinetic energy represents the energy related to the movement of a body. It is calculated as:

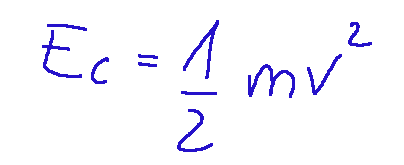
Where:
m = mass of the body
v = velocity of the body

Always in the formula expressed before the potential energy can have two expressions.
for gravity:

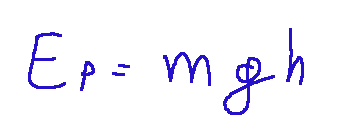
Where:
m = mass of the body
h = height
g = gravitational acceleration

for an ideal spring:

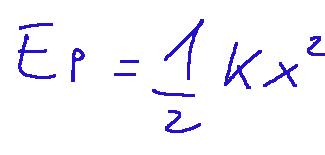
Where:
k = constant elastic
x = deformation of the spring

We can say that it is defined as potential energy UP and is measured in Joules (J), a function of the position related to the work that the body does by moving from position A to B, whatever the points A and B of the path.

Conservative forces
In general, the work that a force does depends on the trajectory followed by the material point. However, there are some forces whose work does not depend on the particular trajectory followed, but only on the initial and final positions (whatever the path followed). These forces are classified as positional forces and among these are conservative forces. All those forces that explicitly depend on time or speed are not positional forces.
There are basically three conservative forces:
-the force of weight
-the elastic force
-the force of gravitational attraction

Non-conservative forces
Non-conservative forces are those forces that dissipate mechanical energy from the system, transforming it into other forms of energy, such as heat. Here is a list of the most studied:
-Friction
-Air resistance
-Internal forces in viscous materials
-Tension forces in ropes and chains with friction
-Damping forces in oscillators

Principle of conservation of mechanical energy
Let's now look in more technical detail at what this important principle of mechanics says.
Given a rigid body or a material point on which a given number of forces act (not necessarily all conservative), mechanical energy E is defined as the quantity obtained by algebraically adding the kinetic energy and the potential energy of each conservative force.
The mechanical energy of a system of forces is a scalar physical quantity, it quantifies the energy possessed by a rigid body or a material point at a precise instant of its motion.
Assuming for hypothesis that all the forces acting on the mechanical system are conservative, then the Principle of Conservation of Mechanical Energy holds: in a mechanical system with ideal constraints, in which the forces are all conservative,
the total mechanical energy remains constant.
This means that, considering any two instants, T1 and T2, of the
motion of a material point, subjected to the action of conservative forces,
the sum of the kinetic energy and the potential energy
at instant T1 is equal to the sum of the same energies at instant T2.
Everything is valid even if the conditions of motion change.
This phenomenon is explained because during the motion the kinetic energy
is transformed into potential energy and vice versa.

The scientists

image created with artificial intelligence, the software used is Microsoft Copilot

The principle of conservation of mechanical energy has been developed through the contribution of several scientists. The best known names are:
-James Prescott Joule, British physicist, known for his experiments on the conversion between mechanical energy and heat
-Hermann von Helmholtz: German physicist and physician
-Julius Robert von Mayer: German physician and physicist

Dynamics and force
The principle of conservation of mechanical energy is closely linked to dynamics and the forces that act on a body. We therefore reiterate the concept of dynamics and force.
Dynamics
Dynamics is a branch of Mechanics. While Kinematics studies motion regardless of what generates it, Dynamics studies the causes that generate motion.
Force
Force is a vector quantity that manifests itself in the interaction between two or more bodies and is defined by Newton's second law. It is possible to distinguish between forces in contact and forces at a distance. It is measured in Newton (N)
Let's remember the following, that is, what 1N is:

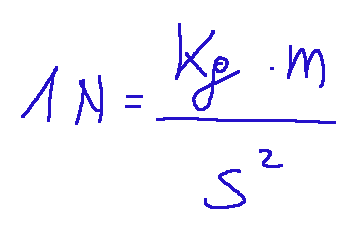
Conclusions
In conclusion, we can say that in the absence of dissipative forces such as friction, the total mechanical energy remains unchanged over time, transforming from one form to another without any loss.

Question
James Prescott Joule made a fundamental contribution to the principle of conservation of energy. Did you know that Joule was so obsessed with his research on energy that he continued to experiment even during his honeymoon?

---

---

ITALIAN

10-04-2025 - Fisica - Conservazione dell’energia meccanica [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_81-80)

Conservazione dell’energia meccanica

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Introduzione
Che consa è la conservazione dell’energia meccanica?
La conservazione dell'energia meccanica è un importate principio della fisica. Questo principio afferma che, in un sistema chiuso e in assenza di forze dissipative, come potrebbe essere l'attrito, l'energia meccanica totale rimane costante nel tempo.
Matematicamente si può esprimere come segue:

Dove:
Em = energia meccanica totale
Ec = energia cinetica
Ep = energia potenziale

Energia cinetica ed energia potenziale
Nella formula espressa prima l'energia cinetica rappresenta l'energia legata al movimento di un corpo. Essa è calcolata come:

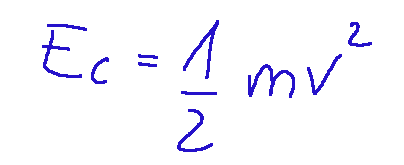
Dove:
m = massa del corpo
v = velocità del corpo

Sempre nella formula espressa prima l'energia potenziale può avere due espressioni.
per gravità:

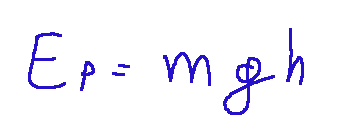
Dove:
m = massa del corpo
h = altezza
g = accelerazione gravitazionale

per una molla ideale:

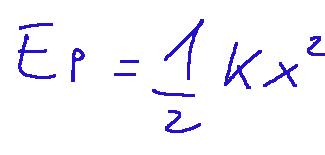
Dove:
k = costante elastica
x = deformazione della molla

Possiamo dire che si definisce energia potenziale UP e si misura in Joule (J), una funzione della posizione legata al lavoro che il corpo compie spostandosi dalla posizione A alla B, qualunque siano i punti A e B del percorso.

Forze conservative
In generale il lavoro che una forza compie dipende dalla traiettoria seguita dal punto materiale. Esistono però alcune forze il cui lavoro non dipende dalla particolare traiettoria seguita, ma soltanto dalla posizione iniziale e da quella finale (qualunque sia il percorso seguito). Tali forze vengono classificate come forze posizionali e fra queste rientrano le forze conservative. Non sono forze posizionali tutte quelle forze che dipendono esplicitamente dal tempo o dalla velocità.
Le forze conservative sono fondamentalmente tre:
-la forza peso
-la forza elastica
-la forza di attrazione gravitazionale

Forze non conservative
Le forze non conservative sono quelle forze che dissipano energia meccanica dal sistema, trasformandola in altre forme di energia, come il calore. Qui di seguito un elenco delle più studiate:
-Attrito
-Resistenza dell'aria
-Forze interne nei materiali viscosi
-Forze di tensione in corde e catene con attrito
-Forze di smorzamento negli oscillatori

Principio di conservazione dell'energia meccanica
Vediamo ora più nel dettaglio tecnico cosa dice questo importante principio della meccanica.
Dato un corpo rigido o un punto materiale su cui agiscono un dato numero di forze (non necessariamente tutte conservative), si definisce energia meccanica E, la grandezza che si ottiene sommando algebricamente l’energia cinetica e l’energia potenziale di ogni forza conservativa.
L’energia meccanica di un sistema di forze è una grandezza fisica scalare, essa quantifica l’energia posseduta da un corpo rigido o da un punto materiale in un preciso istante del suo moto.
Supponendo per ipotesi che tutte le forze agenti sul sistema meccanico siano conservative, allora vale il Principio di Conservazione dell’Energia Meccanica: in un sistema meccanico a vincoli ideali, in cui le forze sono tutte conservative,
l’energia meccanica totale rimane costante.
Questo significa che, considerati due istanti qualunque, T1 e T2, del
moto di un punto materiale, sottoposto all’azione di forze
conservative, la somma dell’energia cinetica e di quella potenziale
all’istante T1 è uguale alla somma delle stesse energie all’istante T2.
Tutto vale anche se le condizioni di moto cambiano.
Questo fenomeno si spiega poiché durante il moto l’energia cinetica
si trasforma in energia potenziale e viceversa.

Gli scienziati

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Il principio di conservazione dell'energia meccanica è si è sviluppato attraverso il contributo di diversi scienziati. I nomi più conosciuti sono:
-James Prescott Joule, fisico britannico, noto per i suoi esperimenti sulla conversione tra energia meccanica e calore
-Hermann von Helmholtz: fisico e medico tedesco
-Julius Robert von Mayer: medico e fisico tedesco

Dinamica e forza
Il principio di conservazione dell'energia meccanica è strettamente legato alla dinamica e alle forze che agiscono su un corpo. Ribadiamo quindi il concetto di dinamica e forza.
La Dinamica
La Dinamica è una branca della Meccanica. Se da un lato la Cinematica studiare il moto a prescindere da ciò che lo genera, in Dinamica si studiano le cause che generano il movimento.
La forza
La forza è una grandezza vettoriale che si manifesta nell'interazione tra due o più corpi e viene definita dalla seconda legge di Newton. È possibile distinguere tra forze a contatto e forze a distanza. Si misura in Newton (N)
Ricordiamo quanto segue, cioè cosa è 1N:

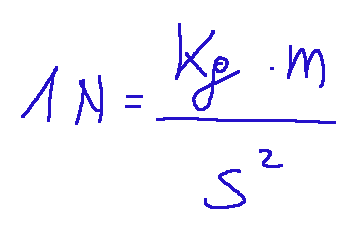
Conclusioni
Concludendo possiamo dire che in assenza di forze dissipative come l'attrito, l'energia meccanica totale rimane invariata nel tempo, trasformandosi da una forma all'altra senza alcuna perdita.

Domanda
James Prescott Joule ha dato un contributo fondamentale per il principio di conservazione dell'energia. Lo sapevate che Joule era talmente ossessionato dalla sua ricerca sull'energia che continuò a fare esperimenti anche durante il viaggio di nozze?

THE END