27-06-2025 - Mathematical Analysis - Exponential and Trigonometric Functions[EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH

27-06-2025 - Mathematical Analysis - Exponential and Trigonometric Functions[EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-91-90)

Exponential and Trigonometric Functions

image created with artificial intelligence, the software used is Microsoft Copilot

Exponential Functions
This type of functions are used to describe phenomena such as growth or decrease.
Exponential functions are the basis for describing more complex functions such as logarithms and probability models.
If we are in the engineering or physics field we will surely find these functions as they have a central role in differential equations.
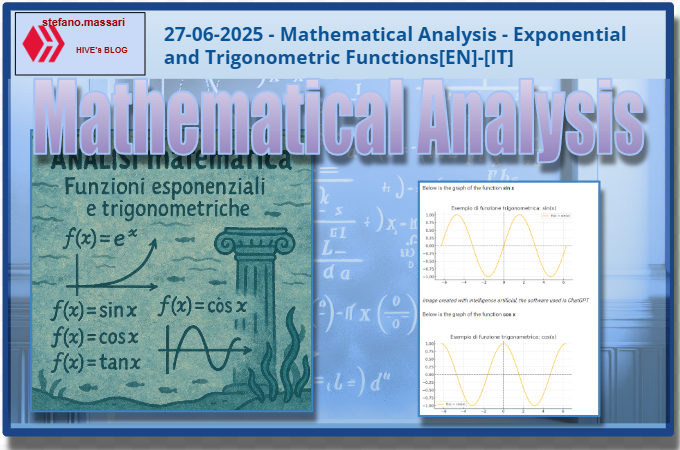
An exponential function is mathematically expressed as follows:

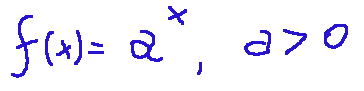
The exponential functions a^x are injective, therefore invertible, for a different from 1.

Below is a graph showing an exponential function.

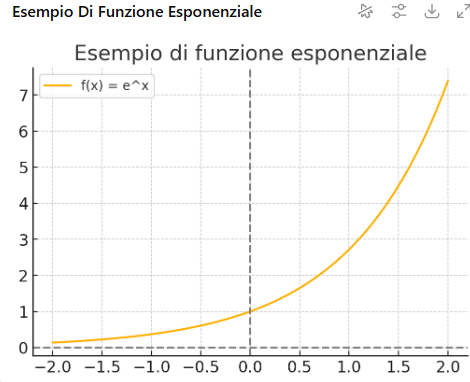
image created with artificial intelligence, the software used is ChatGPT

Logarithmic functions
If we have mentioned exponential functions we cannot fail to mention logarithmic functions.
Let's briefly remember that the logarithm is the function used to find out how many times I have to multiply a number to obtain that other number. It is essentially the opposite of the power.
For example, what is the logarithm to base 2 of 8? the answer is 3, that is, I have to multiply 2 3 times to get 8 (2x2x2=8)

A logarithmic function is defined as follows, I will use a bit of technical language.
We define a logarithmic function based on the inverse function of the exponential a^x.
Mathematically the logarithmic function is expressed as follows.

Below is the graph of a logarithmic function

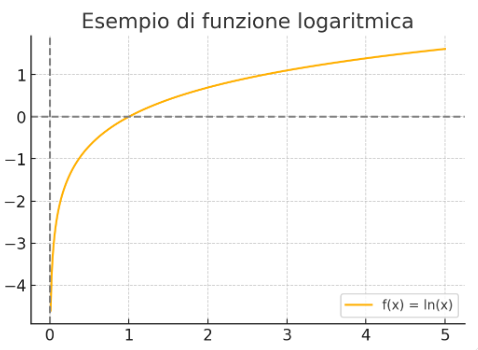
image created with artificial intelligence, the software used is ChatGPT

The graph shows the function of the natural logarithm which would be the logarithm to base e (Euler's number) where e=2.71828

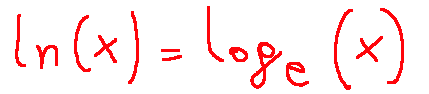
Trigonometric functions
The elementary trigonometric functions are three: sine, cosine and tangent.
They are shown below in their mathematical form.

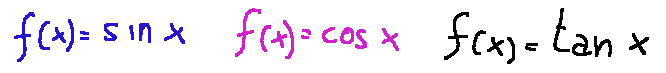
The functions sin x and cos x are defined on the whole set of real numbers and are periodic 2π

Below is the graph of the function sin x

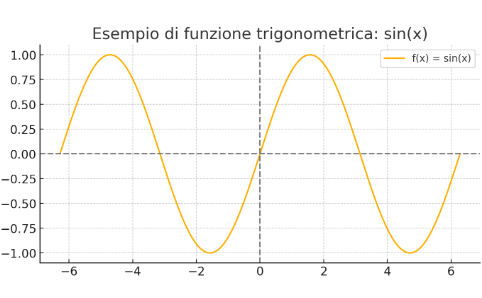
image created with intelligence artificial, the software used is ChatGPT

Below is the graph of the function cos x

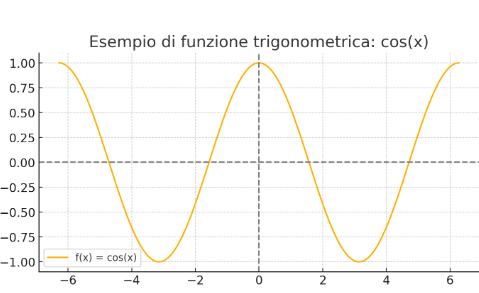
image created with artificial intelligence, the software used is ChatGPT

Below is the graph of the function tan x

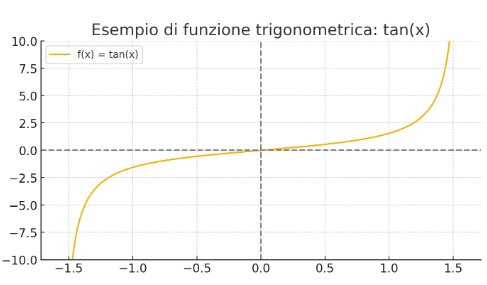
image created with artificial intelligence, the software used is ChatGPT

Conclusions
Exponential and trigonometric functions are part of the elementary functions, that is, they are basic functions of mathematical analysis.
Exponential functions describe growth or decay phenomena. They can be used to analyze the growth of a population or radiative decay.
Trigonometric functions are periodic functions related to the geometry of triangles and are used to describe waves or vibrations.

Question
The term "function", understood as a word, seems to have been born in 1600, but did you know that the trigonometric functions sin, cos, tan, were born from astronomy and the geometry of triangles, well before mathematical analysis? Did you know that the first to use trigonometric functions were the ancient Babylonians?

---

---

ITALIAN

27-06-2025 - Analisi Matematica - Funzioni esponenziali e trigonometriche[EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-91-90)

Funzioni esponenziali e trigonometriche

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Funzioni Esponenziali
Questa tipologia di funzioni vengono usate per descrivere fenomeni come la crescita o la decrescita.
Le funzioni esponenziali sono la base per descrivere funzioni più complesse come logaritmi e modelli di probabilità.
Se siamo nel campo ingegneristico o fisico queste funzioni le ritroveremo sicuramente in quanto hanno un ruolo centrale nelle equazioni differenziali.
Una funzione esponenziale matematicamente è espressa come qui di seguito:

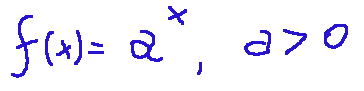
Le funzioni esponenziali a^x sono iniettive, quindi invertibili, per a diverso da 1.

Qui di seguito un grafi che mostra una funzione esponenziale.

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT

Funzioni logaritmiche
Se abbiamo citato le funzioni esponenziali non possiamo non citare le funzioni logaritmiche.
Ricordiamo brevemente che il logaritmo è quella funzione che serve per scoprire quante volte devo moltiplicare un numero per ottenere quell’altro. Sostanzialmente è il contrario della potenza.
Ad esempio quanto è il logaritmo in base 2 di 8? la risposta è 3, cioè devo moltiplicare 3 volte il 2 per ottenere 8 (2x2x2=8)

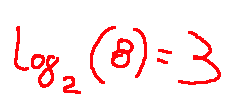
Una funzione logaritmica è definita come segue, userò un linguaggio un po' tecnico.
Definiamo una funzione logaritmica in base a la funzione inversa dell'esponenziale a^x.
Matematicamente la funzione logaritmica viene espressa come segue.

Qui di seguito il grafico di una funzione logaritmica

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT

Il grafico mostra la funzione del logaritmo naturale che sarebbe il logaritmo in base e (numero di Eulero) dove e=2,71828

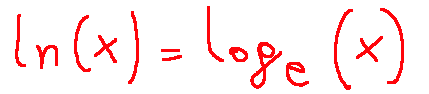
Funzioni trigonometriche
Le funzioni trigonometriche elementari sono tre: seno, coseno e tangente.
Qui di seguito sono mostrate nella loro forma matematica.

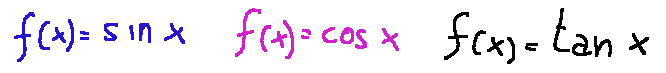
Le funzioni sin x e cos x sono definite su tutto l'insieme dei numeri reali e sono periodiche 2π

Qui di seguito il grafico della funzione sin x

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT

Qui di seguito il grafico della funzione cos x

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT

Qui di seguito il grafico della funzione tan x

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT

Conclusioni
Le funzioni esponenziali e trigonometriche fanno parte delle funzioni elementari, ovvero sono funzioni base dell'analisi matematica.
Le funzioni esponenziali descrivono fenomeni di crescita o decadimento. Possono essere usate per analizzare la crescita di una popolazione o il decadimento radiativo.
Le funzioni trigonometriche sono funzioni periodiche legate alla geometria dei triangoli e sono usate per descrivere le onde o le vibrazioni.

Domanda
Il termine "funzione", inteso proprio come parola sembra che sia nato nel 1600, ma lo sapevate che le funzioni trigonometriche sin, cos, tan, nascono dall’astronomia e dalla geometria dei triangoli, ben prima dell’analisi matematica? Lo sapevate che i primi ad usare le funzioni trigonometriche furono gli antichi Babilonesi?

THE END