03-07-2025 - Mathematical Analysis - Continuous Functions [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH

03-07-2025 - Mathematical Analysis - Continuous Functions [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-79)

Continuous Functions

image created with artificial intelligence, the software used is Microsoft Copilot

Definition of continuous function
A continuous function is said to be when f is continuous in x0 if the following relation exists mathematics:

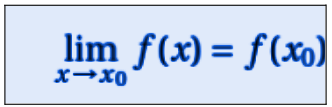
The above is the formal definition of continuity of a function at a point. It basically means that f(x) is continuous at the point x0 if the limit of f(x) as x tends to x0 exists and is equal to the value of the function at that point.

Below is a graphical example of a continuous function

Below is the graph of the function…

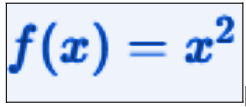
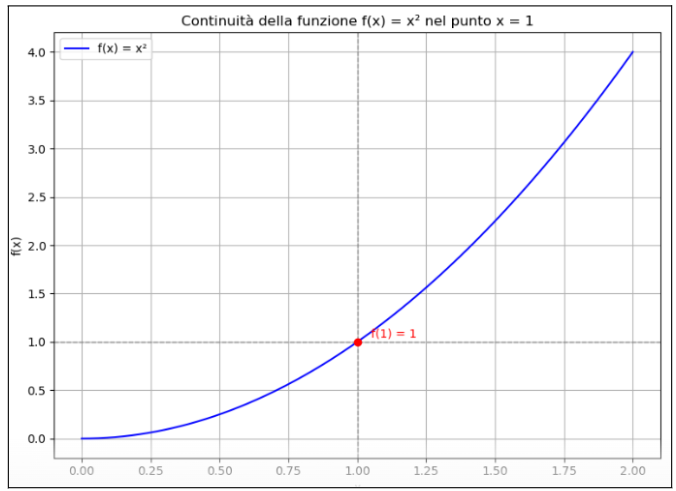
image created with artificial intelligence, the software used is Microsoft Copilot

The graph illustrates that the function f(x) = x^2 and its continuity at the point x = 1
What can we see in the graph
The blue curve represents the function f(x)=x^2 and the red dot indicates that f(1)=1. In the graph there are also some gray dotted lines, they show how the limit for x→1 coincides with the value of the function at that point.
What we have said is described mathematically in the following way.

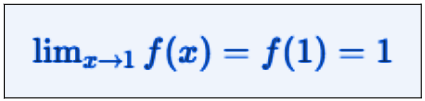
Continuous function, simple description
In simple words, a function is continuous at a point if you can draw it without lifting the pen from the paper at that point. This means that if we look at the graph of the function near a certain point, there are no interruptions.
Below I also explain what a discontinuous function is to better clarify the concept of a continuous function.

Discontinuous function
A discontinuous function is a function that shows a graph with one or more interruptions. Simply, if we have to draw the graph of a discontinuous function with a pen, we must lift the pen from the paper to report it correctly.
So a discontinuous function has at least one interruption at one point.
Below is an example.
Let's consider the function defined as:

Below is the graph of the function described above

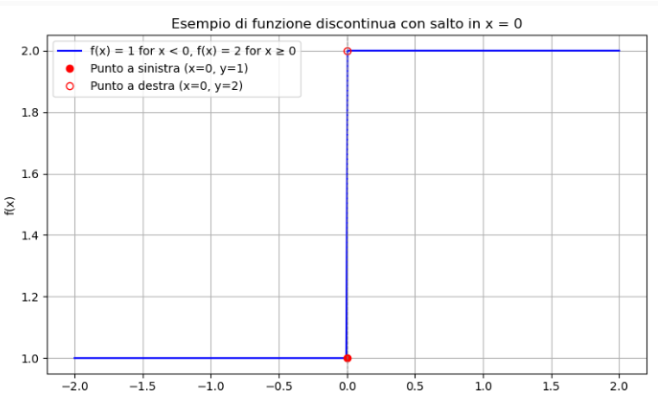
image created with artificial intelligence, the software used is Microsoft Copilot

So this is a piecewise function that has a discontinuity at x = 0. In this case we speak of jump discontinuity.
The left limit is equal to 1, while the right limit is 2.

Conclusions
Continuous and discontinuous functions are useful for modeling natural phenomena, calculating integrals and seeking optimization in analytical models.

Question
Continuous functions were used scientifically already in the 17th century by Newton and Leibniz, but did you know that their rigorous definition came only two centuries later with the French mathematician Cauchy?

ITALIAN

03-07-2025 - Analisi Matematica - Funzioni continue [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-79)

Funzioni continue

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Definizione di funzione continua
Si dice funzione continua quando f è continua in x0 se esiste la seguente relazione matematica:

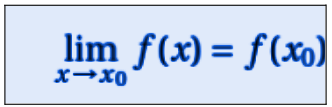
Quello descritto sopra è la definizione formale di continuità di una funzione in un punto. Sostanzialmente significa che la f(x) è continua nel punto x0 se il limite di f(x) per x che tende a x0 esiste ed è uguale al valore della funzione in quel punto.

Qui di seguito un esempio grafico di funzione continua

Qui Sotto il grafico della funzione…

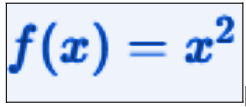
immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Il grafico illustra che la funzione f(x) = x^2 e la sua continuità nel punto x = 1
Cosa possiamo vedere nel grafico
La curva blu rappresenta la funzione f(x)=x^2 ed il punto rosso segnala che f(1)=1. Nel grafico sono presenti anche delle linee tratteggiate grigie, esse mostrano come il limite per x→1 coincide con il valore della funzione in quel punto.
Quello che abbiamo detto si descrive matematicamente nella seguente maniera.

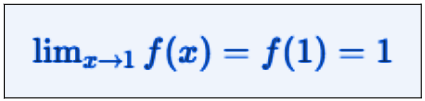
Funzione continua, descrizione semplice
In parole semplici una funzione è continua in un punto se puoi disegnarla senza staccare la penna dal foglio in quel punto. Questo significa che se guardiamo il grafico della funzione vicino ad un determinato punto, non ci sono interruzioni.
Qui di seguito spiego anche cosa è una funzione discontinua per chiarire meglio anche il concetto di funzione continua.

Funzione discontinua
Una funzione discontinua è una funzione che mostra un grafico con una o più interruzioni. Semplicemente, se dobbiamo disegnare il grafico di una funzione discontinua con una penna, dobbiamo staccare la penna dal foglio per riportarla correttamente.
Quindi una funzione discontinua presenta almeno un'interruzione in un punto.
Qui di seguito un esempio.
Prendiamo in considerazione la funzione definita come:

Qui di seguito il grafico della funzione descritta sopra

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Quindi questa è una funzione a tratti che presenta un discontinuità in x = 0. In questo caso parliamo di discontinuità di salto.
Il limite sinistro è uguale a 1, mentre il limite destro è 2.

Conclusioni
Le funzioni continue e discontinue sono utili per modellare fenomeni naturali, calcolare integrali e cercare l’ottimizzazione nei modelli analitici.

Domanda
Le funzioni continue erano usate in maniera scientifica già nel XVII secolo da Newton e Leibniz, ma lo sapevate che la loro definizione rigorosa è arrivata solo due secoli dopo con il matematico francese Cauchy?

THE END