30-08-2025 - Operations Research - Maximum Number of Solutions [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH

30-08-2025 - Operations Research - Maximum Number of Solutions [EN]-[IT]
With this post, I would like to provide a brief introduction to the topic in question.
(lesson/article code: QE_11)

Image created with artificial intelligence, the software used is Microsoft Copilot

Introduction
Linear programming is a mathematical tool used to optimize decisions.

It is used when the problems being analyzed present constraints and particular conditions. It is used in manufacturing to maximize profit or minimize costs.

Application Example
Below is an example of a linear programming problem.

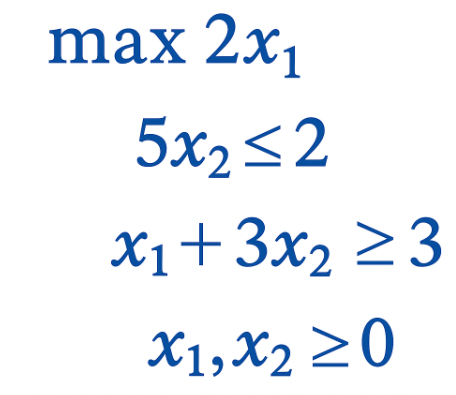
The first line immediately defines the objective function, which is to maximize 2x1.

The Constraints
The constraints are that 5x2 must be less than or equal to 2, then that x1 + 3x2 must be greater than or equal to 3, and that x1, x2 cannot be negative numbers.

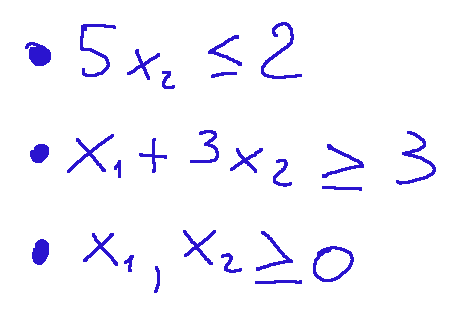
Maximum number of basic solutions
The number of possible combinations of active constraints determines the maximum number of basic solutions to a linear programming problem.
First, we need to think about how many constraints we have.

Constraint 1
This constraint limits the value of x2, and if we rewrite it, we could represent it as follows:

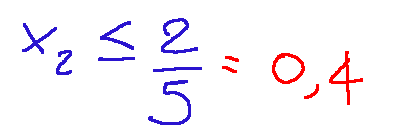
Constraint 2

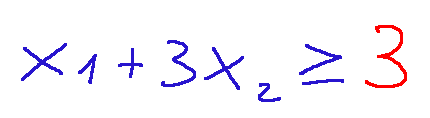
This constraint is of the greater-than-equal type, so This means that the feasible region lies above the line (this is a bit technical, but next time I'll try to better explain that the problem we're tackling can be represented on a graph).

Isolating x1, we get the following:

Constraint 3

X1 cannot be negative

Constraint 4

X2 cannot be negative

The reasoning
We have two fundamental questions:
1-Each pair of constraints can generate an intersection point.
2-We have 4 constraints (excluding the objective function).

So the maximum number of intersections between pairs of constraints is:

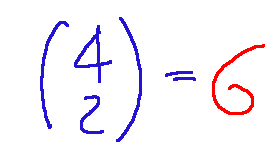
Note: This is a mathematical combination read as 4 out of 2, or a combination of 4 elements taken two at a time.

The combination is calculated with the following formula:

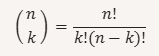
and in our case it becomes as follows:

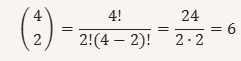
Answer
6 is the theoretical maximum number of basic solutions, i.e., the maximum number of vertices that the A feasible polygon can have.

Graphically, the linear programming problem looks like this:

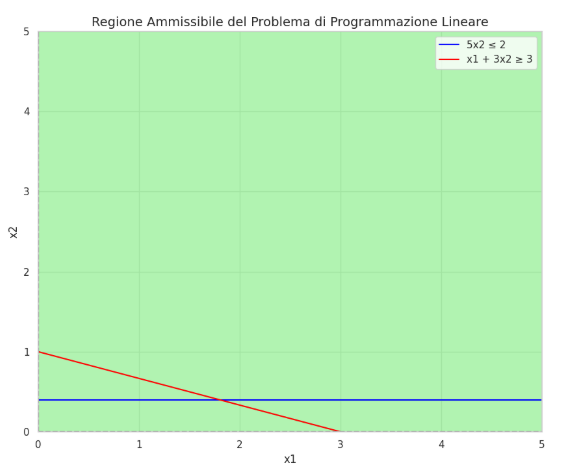
Image created with artificial intelligence, the software used is Microsoft Copilot

Where:
The blue line represents the first constraint x2<=0.4
The red line represents the constraint 𝑥1+3𝑥2≥3, meaning the region lies above this line.

The feasible region is the blue one indicated in the graph below, and we can see that it is unbounded to the right.

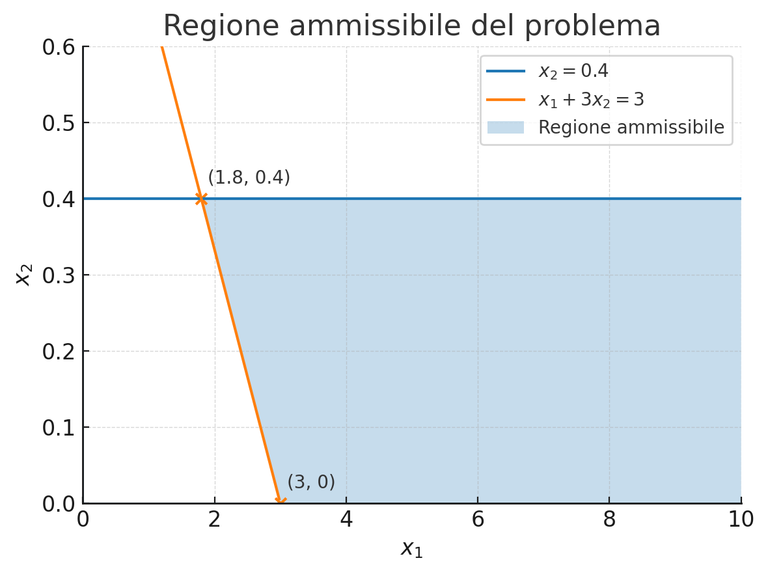
Conclusions
Linear programming is used in finance, logistics, industry, agriculture, and marketing. When tackling complex linear programming problems, we know there's a method that helps us identify the maximum number of basic solutions, or the maximum number of possible choices.

Question
Did you know that the concept of "maximum number of basic solutions" isn't that old? Did you know it was introduced around 1950 by American mathematician George Dantzig?

---

---

ITALIAN

30-08-2025 - Ricerca operativa - Numero massimo di soluzioni [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(codice lezione/articolo: QE_11)

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Introduzione
La programmazione lineare è uno strumento matematico che viene usato per ottimizzare decisioni.
Viene usata quando i problemi da analizzare presentano dei vincoli e particolari condizioni. Viene usata nell'ambito produttivo per trovare il massimo profitto oppure per minimizzare i costi.

Esempio di applicazione
Qui di seguito un esempio di un problema di programmazione lineare.

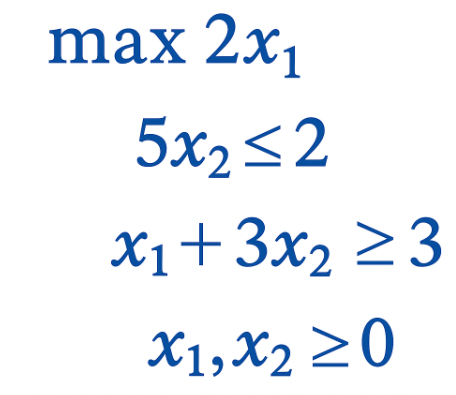
La prima riga ci definisce subito la funzione obiettivo che risulta essere massimizzare 2x1

I vincoli
I vincoli sono che 5x2 deve essere minore o uguale a 2, poi che x1+3x2 deve essere maggiore o uguale a 3 e che x1,x2 non possono essere numeri negativi.

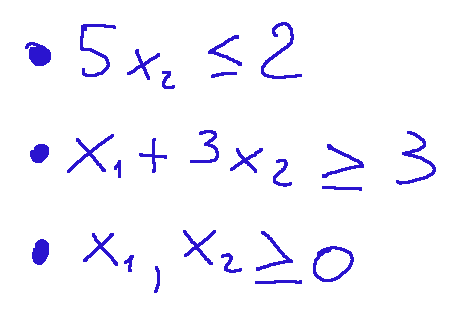
Numero massimo di soluzioni base
Il numero di combinazioni possibili tra i vincoli attivi determinano il numero massimo di soluzioni di base di un problema di programmazione lineare.
Prima di tutto dobbiamo ragionare su quanti vincoli abbiamo.

Vincolo 1
Questo vincolo da un limite al valore di x2 e se lo riscriviamo potremmo rappresentarlo nella seguente maniera:

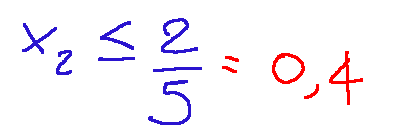
Vincolo 2

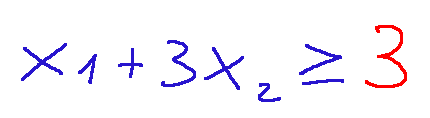
Questo vincolo è di tipo maggiore uguale, quindi vuol dire che la regione ammissibile si trova sopra la retta (questo è un linguaggi un po' tecnico, ma la prossima volta proverò a spiegare meglio che il problema che stiamo affrontando si può rappresentare su un grafico)

Andando ad isolare x1 avremo quanto segue:

Vincolo 3

X1 non può essere negativo

Vincolo 4

X2 non può essere negativo

Il ragionamento
Abbiamo due questioni fondamentali:
1-Ogni coppia di vincoli può generare un punto di intersezione.
2-Abbiamo 4 vincoli (escludendo la funzione obiettivo).

Quindi il numero massimo di intersezioni tra coppie di vincoli è:

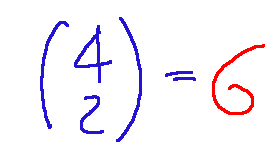
Nota: questa è una combinazione matematica che si legge 4 su 2, oppure combinazione di 4 elementi presi 2 alla volta.

La combinazione si calcola con la seguente formula:

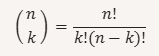
e nel nostro caso diventa come segue:

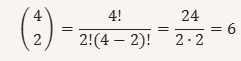
Risposta
6 è il numero massimo teorico di soluzioni di base, cioè il numero massimo di vertici che il poligono ammissibile può avere.

Graficamente il problema di programmazione lineare si presenta come di seguito

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Dove:
La linea blu rappresenta il primo vincolo x2<=0,4
La linea rossa rappresenta il vincolo 𝑥1+3𝑥2≥3, ovvero la regione si trova sopra questa retta.

La regione ammissibile è quella azzurra segnalata dal grafico qui sotto riportato e possiamo notare che la regione è illimitata verso destra

Conclusioni
La programmazione lineare si applica in finanza, nella logistica, nell'industria, in agricoltura e nel marketing. Quando si affrontano problemi di programmazione lineare complessi, sappiamo che c'è un metodo che ci aiuta ad identificare il numero massimo di soluzioni di base, ovvero il massimo numero di scelte possibili.

Domanda
Sapevate che il concetto di "numero massimo di soluzioni di base" non è tanto vecchio? Sapevate che fu introdotto circa nel 1950 dal matematico statunitense George Dantzig?

THE END