30-06-2025 - Mathematical Analysis - Function Limits [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH

30-06-2025 - Mathematical Analysis - Function Limits [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X-89)

Function Limits

image created with artificial intelligence, the software used is Microsoft Copilot

Introduction
When we are in mathematical analysis and we talk about function limits, we can say that the limit of a function describes the behavior of the values ​​of the function when the independent variable approaches a certain point, but at that point the function is not defined.

Definition
Technically we can define the limit of a function as follows:
Let...

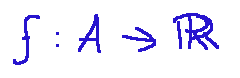
... be a function defined on a subset A of the real numbers and let x0 be an accumulation point for A. It is said that the function f admits a limit l for x that tends to x0 and is written as following:

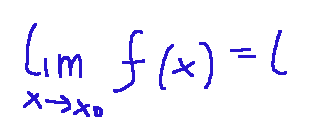
We can repeat this in a slightly different way
Let's imagine a graph of f(x)
In this graph, if we get closer with x to a certain value c, the corresponding f(x) get closer and closer to a number L let's say that:

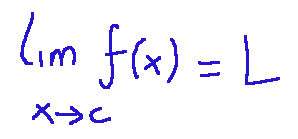
Limit and infinity

Be careful, this concept is also valid when x grows without limits, that is, it tends to +∞ or -∞. When we enter these cases we talk about limits at infinity.
Technically we can say the following:
It is said that...

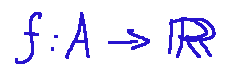
...tends to +∞ for x-->0, being x0 accumulation point for A and it will be written as follows:

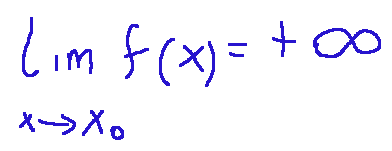
Study of a function
Let's think about the following function

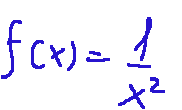
Here is the graph of the function:

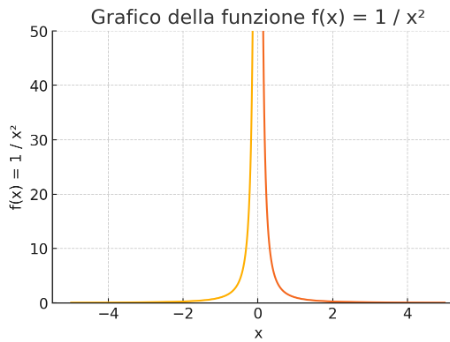
image created with artificial intelligence, the software used is ChatGPT

Note that the values ​​are symmetric, there are two branches that provide to the function a property, namely that it is an even function.
There is a singularity at x = 0. The values ​​that approach zero explode towards +∞

For ∣x∣ --> ∞ the curve drops and tends to 0, so the x-axis is a horizontal asymptote.

Right limit and left limit
The limits can be right and left and are written in the following way.

Left Limit
The left limit of f(x) at the point c is written as follows:

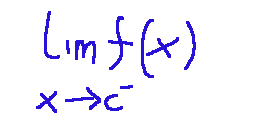
Here we observe the values ​​of the function as x approaches C for smaller values, that is, from the left on the x-axis.

Right Limit
The right limit of f(x) at point c is written as follows:

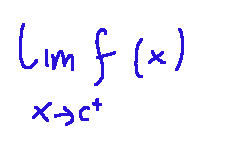
Here we observe the values ​​of the function when x approaches C for larger values, that is, from the right.

Example
Let's try to understand what is the limit for x tending to 3+ of...

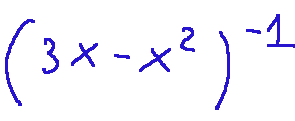
that is, mathematically we want to look for this:

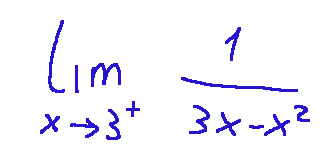
this represents the right limit of the function...

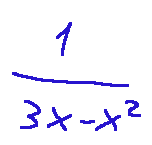
when x approaches 3 from larger values.

development
the function is the following:

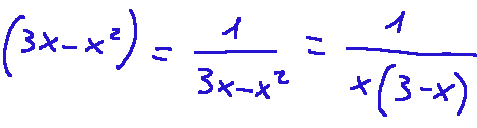
now let's study the behavior for...

for x > 3 we have:
X>0 (positive)
3-x<0 (negative, but with very small absolute value)

We can therefore arrive at the consideration that x(3-x) is negative and very close to 0.

that is...

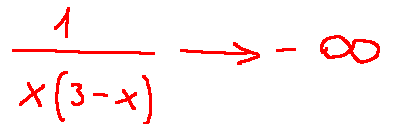
Result
Therefore the limit for x tending to 3+ of...

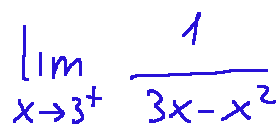
is exactly - infinity:

Conclusions
The study of limits is one of the fundamental bases of mathematical analysis. These particular studies are useful to define continuity if a function does not break at a point, to calculate derivatives, to study behaviors at the extremes and to understand physical phenomena.
Finally, the study of limits is useful to analyze asymptotes (invisible lines to which a curve gets closer and closer) and discontinuities.

Question
Have you ever heard of the French mathematician Augustin-Louis Cauchy (1789–1857)?
Did you know that it was Cauchy who gave a more rigorous definition of limit and who introduced the idea that a variable could get indefinitely close to a value?

---

---

ITALIAN

30-06-2025 - Analisi Matematica - Limiti di funzioni [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-89)

Limiti di funzioni

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Introduzione
Quando siamo in analisi matematica e parliamo di limiti di funzione, possiamo dire che il limite di una funzione descrive il comportamento dei valori della funzione quando la variabile indipendente si avvicina ad un certo punto, ma in quel punto la funzione non è definita.

Definizione
In maniera tecnica possiamo definire il limite di funzione come segue:
Sia...

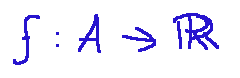
... una funzione definita su un sottoinsieme A dei reali e sia x0 un punto di accumulazione per A. Si dice che la funzione f ammette limite l per x che tende a x0 e si scrive nella maniera seguente:

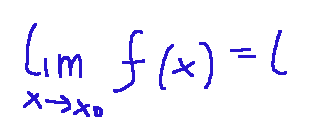
Possiamo ripeterlo in una maniera leggermente diversa
Immaginiamo un grafico di f(x)
In questo grafico, se avvicinandoci con x a un certo valore c, i corrispondenti f(x) si avvicinano sempre di più a un numero L diciamo che:

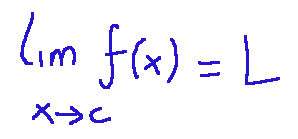
Limite e infinito

Attenzione, questo concetto vale anche quando x cresce senza limiti, cioè tende a +∞ o a -∞. Quando entriamo in questi casi parliamo di limiti all'infinito.
Tecnicamente possiamo dire quanto segue:
Si dice che...

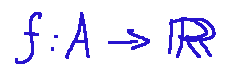
...tende a +∞ per x-->0, essendo x0 punto di accumulazione per A e si scriverà così:

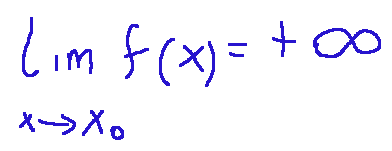
Studio di una funzione
Proviamo a pensare alla seguente funzione

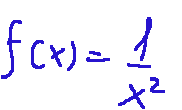
Qui di seguito il grafico della funzione:

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT

Notiamo che i valori sono simmetrici, ci sono due rami che forniscono alla funzione una proprietà, cioè che è una funzione pari.
C'è una singolarità in x = 0. I valori che si avvicinano allo zero esplodono verso +∞

Per ∣x∣ --> ∞ la curva scende e tende a 0, perciò l'asse x è un asintoto orizzontale.

Limite destro e limite sinistro
Il limiti possono essere destri e sinistri e si scrivono nella seguente maniera.

Limite sinistro
Il limite sinistro di f(x) nel punto c si scrive come segue:

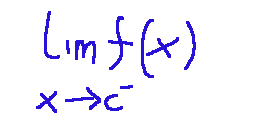
Qui osserviamo i valori della funzione quando x si avvicina a C per valori minori, cioè da sinistra sull'asse x.

Limite destro
Il limite destro di f(x) nel punto c si scrive come segue:

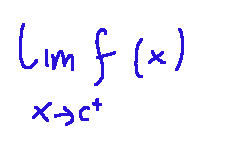
Qui osserviamo i valori della funzione quando x si avvicina a C per valori maggiore, cioè da destra.

Esempio
Proviamo a capire qual è il limite per x che tende a 3+ di...

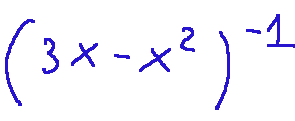
ovvero, matematicamente vogliamo cercare questo:

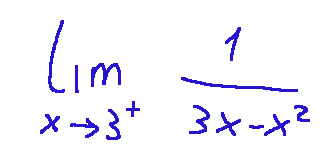
questo rappresenta il limite destro della funzione...

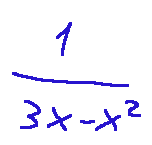
quando x si avvicina a 3 da valori maggiori.

sviluppo
la funzione è la seguente:

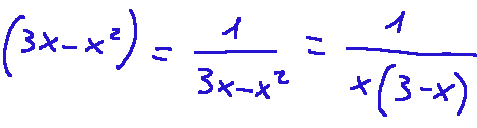
ora studiamo il comportamento per...

per x > 3 abbiamo:
X>0 (positivo)
3-x<0 (negativo, ma con valore assoluto piccolissimo)

Possiamo quindi arrivare alla considerazione che x(3-x) è negativo e molto vicino a 0.

cioè...

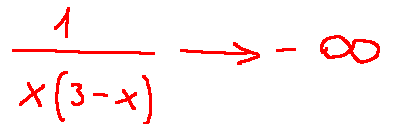
Risultato
Quindi il limite per x che tende a 3+ di...

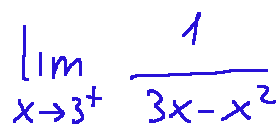
è esattamente - infinito:

Conclusioni
Lo studio dei limiti è una delle basi fondamentali dell'analisi matematica. Questi particolari studi servono a definire la continuità se una funzione non si spezza in un punto, a calcolare derivate, a studiare i comportamenti agli estremi e a comprendere i fenomeni fisici.
Infine lo studio dei limiti è utile per analizzare gli asintoti (linee invisibili a cui una curva si avvicina sempre di più) e le discontinuità.

Domanda
Avete mai sentito parlare del matematico francese Augustin-Louis Cauchy (1789–1857)?
La sapevate che fu proprio Cauchy a dare una definizione più rigorosa di limite e che introdusse l’idea che una variabile potesse avvicinarsi indefinitamente ad un valore?

THE END