27-11-2023 - Mechanical drawing - Tolerance exercise [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
27-11-2023 - Mechanical drawing - Tolerance exercise [EN]-[IT]

Exercise on dimensional tolerances
Dimensional tolerances are a tool for defining allowable machining errors on components. The other two tools, in addition to dimensional tolerances, are roughness parameters and geometric tolerances.
Dimensional tolerance decides the degree of fit. We know that it is possible to obtain the same type of coupling by imposing different tolerance torques on the pieces.
Below we will analyze a pairing.

Mate Analysis 12 - JS9/h9
First of all in this particular situation we can immediately see that we have a JS tolerance, a tolerance that is symmetric about zero.

The first thing we need to do is to obtain the amplitudes of the two tolerances and we can do this by looking at table one of the UNI EN 20286‐1 ISO system of tolerances and couplings. Fundamental principles for tolerances, deviations and fits.

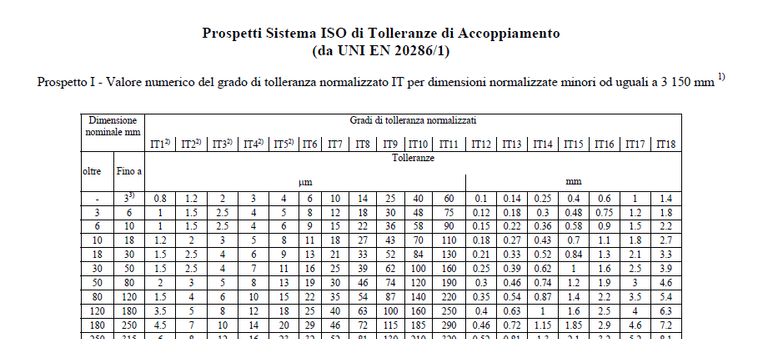
From this table we have the following data:
For a 12mm size the JS9 tolerance has a range of 43μ
For a 12mm size the h9 tolerance has a range of 43μ

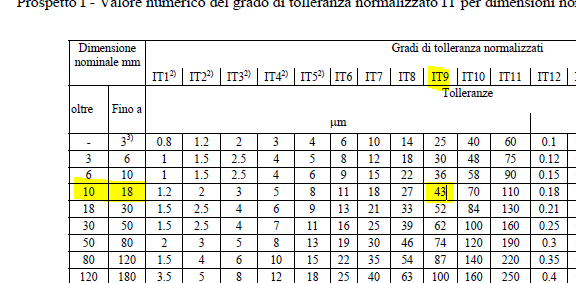
Then we go to see where the points closest to the zero line of both tolerances are located and to do this we will always use the tables included in the UNI 20286-1 standard

For dimension 12 JS9 we have that the lower bound is ITn/2 = 21.5 μ
For the dimension 12 h9 we have that the lower limit is 0 μ

We will therefore have that the lower end of the hole of 12 JS9 will be at 21.5 μ above the zero line, while the lower end of the shaft of 12 JS9 will be at 0 μ, therefore on the zero line

We can now calculate the other extremes.
Upper bound of 12 JS9 is ITn/2 = 21.5 μ
Upper bound of 12 h9 is lower bound + IT = 43 μ

Graphically we can represent the situation in the following way:

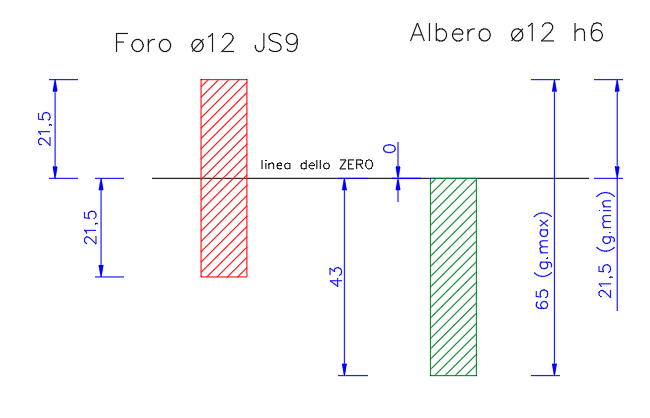
The maximum clearance will be 65 μ
The minimum clearance will be 21.5 μ
Maximum interference will be 21.5 μ

In this case we have an uncertain coupling.

Conclusions
Dimensional tolerances have the function of identifying the type of coupling between a hole and a shaft. Mates can be with play, with interference or uncertain.

---

---

ITALIAN
27-11-2023 - Disegno meccanico - Esercizio sulle tolleranze [EN]-[IT]

Esercizio sulle tolleranze dimensionali
Le tolleranze dimensionali sono uno strumento per definire gli errori di lavorazione ammissibili sui componenti. Gli altri due strumenti, oltre alle tolleranze dimensionali, sono i parametri di rugosità e le tolleranze geometriche.
La tolleranza dimensionale decide il grado di accoppiamento. Sappiamo che è possibile ottenere il medesimo tipo di accoppiamento imponendo ai pezzi diverse coppie di tolleranza.
Qui di seguito andremo ad analizzare un accoppiamento.

Analisi dell'accoppiamento 12 - JS9/h9
Prima di tutto in questa particolare situazione possiamo vedere subito che abbiamo una tolleranza JS, una tolleranza simmetrica rispetto allo zero.

La prima cosa che dobbiamo fare è andare a ricavare le ampiezze delle due tolleranze e questo lo possiamo fare andando a vedere il prospetto uno della norma UNI EN 20286‐1 Sistema ISO di tolleranze ed accoppiamenti. Principi fondamentali per tolleranze, scostamenti ed accoppiamenti.

Da questo prospetto abbiamo i seguenti dati:
Per una dimensione di 12 mm la tolleranza JS9 ha un intervallo di 43μ
Per una dimensione di 12 mm la tolleranza h9 ha un intervallo di 43μ

Poi andiamo a vedere dove si trovano i punti più vicini alla linea di zero di entrambe le tolleranze e per fare questo useremo sempre le tabelle inserite nella norma UNI 20286-1

Per la dimensione 12 JS9 abbiamo che l'estremo inferiore è ITn/2 = 21,5 μ
Per la dimensione 12 h9 abbiamo che l'estremo inferiore è a 0 μ

Avremo quindi che l'estremo inferiore del foro di 12 JS9 sarà a 21,5 μ sopra la linea di zero, mentre l'estremo inferiore dell'albero di 12 JS9 sarà a 0 μ, quindi sulla linea di zero

Ci possiamo calcolare ora gli altri estremi.
Estremo superiore di 12 JS9 è ITn/2 = 21,5 μ
Estremo superiore di 12 h9 è estremo inferiore + IT = 43 μ

Graficamente possiamo rappresentare la situazione nella seguente maniera:

Il gioco massimo sarà di 65 μ
Il gioco minimo sarà di 21,5 μ
Interferenza massima sarà di 21,5 μ

In questo caso abbiamo un accoppiamento incerto.

Conclusioni
Le tolleranze dimensionali hanno la funzione di identificare la tipologia di accoppiamento tra un foro ed un albero. Gli accoppiamenti possono essere con gioco, con interferenza o incerti.

THE END