14-09-2025 - Operations Research - Standard Linear Programming [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH

14-09-2025 - Operations Research - Standard Linear Programming [EN]-[IT]
With this post, I would like to provide a brief introduction to the topic mentioned above.
(lesson/article code: MS_08)

Image created with artificial intelligence, the software used is Microsoft Copilot

Introduction
Today, I'll try to provide a simple example of a linear programming problem in standard form.
First of all, let's say that linear programming is a mathematical tool used to optimize decisions after analyzing certain constraints. Linear programming helps find the best possible combination given a certain number of variables and constraints.
A linear programming problem is therefore made up of an objective function and a set of constraints.

Example
Suppose we want to solve the following maximization problem.

objective function

Constraints
Here are the constraints of our problem.

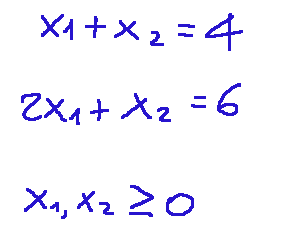
matrix form
Linear programming can also be viewed in matrix form.

Below is the linear programming problem in matrix form.

Objective function

Coefficient matrix

Terms known

Variables

Fit issue standard

Graph

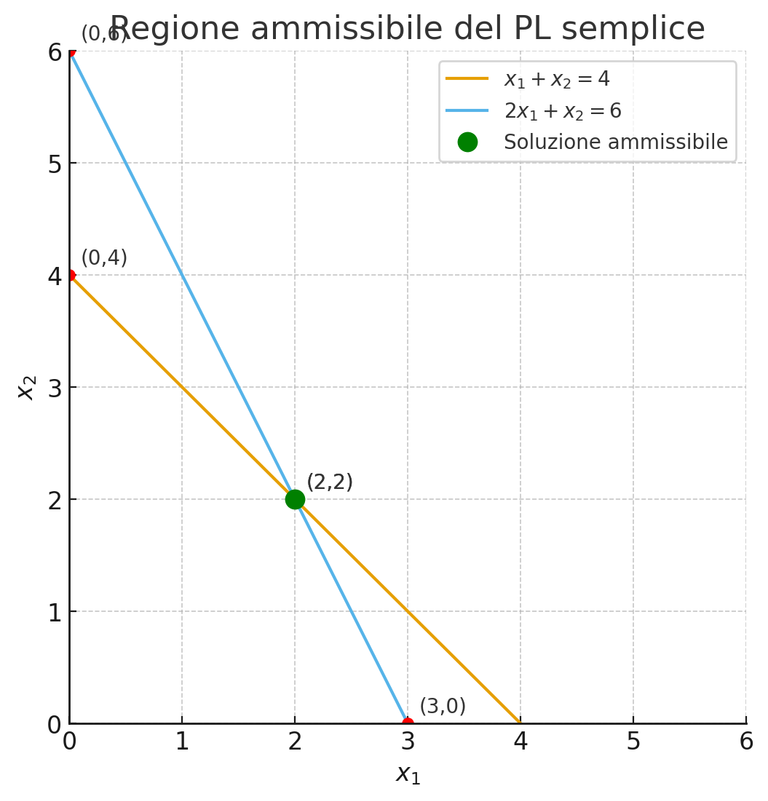
Image created with artificial intelligence, ChatGPT software used

To plot the lines in the graph, we need to use the two given constraints listed below.

Now we need to find the points of intersection with the axes by performing the following operations:
The x1 intercept: setting x2=0, we find x1
The x2 intercept: setting x1=0, we find x2

For

we will have

For

we will have

So we have two lines, and we can see them plotted in the graph above. The lines are as follows:
Line passing through (0,4) and (4,0) [in the graph, it's the orange one]
Line passing through (0,6) and (3,0) [in the graph, it's the blue one]

By plotting the lines in the graph, we find the point of intersection of the lines, and in this example, the feasible region is reduced to a single point (2,2), which also represents the solution to this linear programming problem.
Below is the graph showing the result.

This means that to solve our objective function shown below,

And given these Constraints

The solution to the system is point (2,2)

The exercise is finished, but here's the explanation with the system of equations
NOTE:
To solve the system of equations, we can proceed with substitution, as follows:

Isolate a variable from the first equation (1), and then from equation 1 we will have: follows:

Substitute into the second equation and simplify.

we find x2

and we have the solution.

Conclusions
In this post, I've shown a linear programming exercise that we can consider relatively simple. In this case, the feasible region is just one point, namely (2,2), which also represents the solution to the linear programming problem.

Question
Did you know that linear programming was invented by the American mathematician George Bernard Dantzig (1914–2005)? Did you know that all of Dantzig's work was inspired by his assignment in the U.S. Air Force from 1941 to 1946?

---

---

ITALIAN

14-09-2025 - Ricerca operativa - Programmazione Lineare standard [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(codice lezione/articolo: MS_08)

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Introduzione
Oggi provo a riportare un esempio semplice di problema di Programmazione Lineare in forma standard.
Innanzi tutto diciamo che la programmazione lineare è uno strumento matematico usato per ottimizzare decisioni da prendere dopo aver analizzato determinati vincoli. La programmazione lineare aiuta a trovare la miglior combinazione possibile dato un certo numero di variabili e di vincoli.
Un problema di programmazione lineare è quindi formato da una funzione obiettivo e da una serie di vincoli.

Esempio
Supponiamo di voler risolvere il seguente problema di massimizzazione.

funzione obiettivo

I vincoli
Qui di seguito i vincoli del nostro problema.

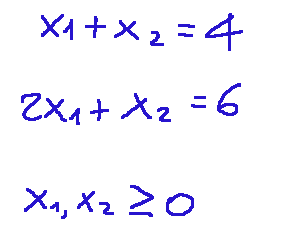
forma matriciale
La programmazione lineare può essere vista anche in forma matriciale.
Qui di seguito riporto il problema di programmazione lineare in forma matriciale.

Funzione obiettivo

Matrice dei coefficienti

Termini noti

Variabili

Problema in forma standard

Grafico

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT

Per tracciare le rette del grafico dobbiamo riprendere i due vincoli dati che riporto qui sotto.

ora dobbiamo ricavare i punti di intersezione con gli assi eseguendo le seguenti operazioni:
L'intercetta su x1: ponendo x2=0 troviamo x1
L'intercetta su x2: ponendo x1=0 troviamo x2

Per

avremo

per

avremo

Quindi avremo due rette e queste le possiamo vedere tracciate nel grafico sopra inserito, le rette sono le seguenti:
Retta che passa per (0,4) e (4,0) [nel grafico è quella arancione]
Retta che passa per (0,6) e (3,0) [nel grafico è quella azzurra]

Tracciando le rette nel grafico troviamo il punto di intersezione delle linee ed in questo esempio la regione ammissibile è ridotta a un solo punto (2,2), che rappresenta anche la soluzione di questo problema di programmazione lineare.
Qui di seguito riporto il grafico indicando il risultato

Questo significa che per risolvere la nostra funzione obiettivo riportata qui sotto

e dati questi vincoli

la soluzione al sistema è il punto (2,2)

L'esercizio è finito, ma di seguito la spiegazione con il sistema di equazioni
NOTA:
Per risolvere il sistema di equazione possiamo procedere con la sostituzione, cioè come segue:

si isola una variabile della prima equazione (1) e quindi dalla 1 avremo quanto segue:

Sostituiamo nella seconda equazione e semplifichiamo

troviamo x2

e abbiamo la soluzione

Conclusioni
In questo post ho mostrato un esercizio di programmazione lineare che possiamo considerare relativamente semplice. In questo caso la regione ammissibile è solo un punto, cioè (2,2) che rappresenta anche la soluzione del problema di programmazione lineare.

Domanda
Sapevate che la programmazione lineare fu inventata dal matematico statunitense George Bernard Dantzig (1914–2005)? Sapevate che tutto il lavoro di Dantzig fu ispirato dall'incarico che ebbe nell’U.S. Air Force dal 1941 al 1946?

THE END