11-07-2025 - Mathematical Analysis - Integrals of rational functions [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

11-07-2025 - Mathematical Analysis - Integrals of rational functions [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X-60-59)
Integrals of rational functions
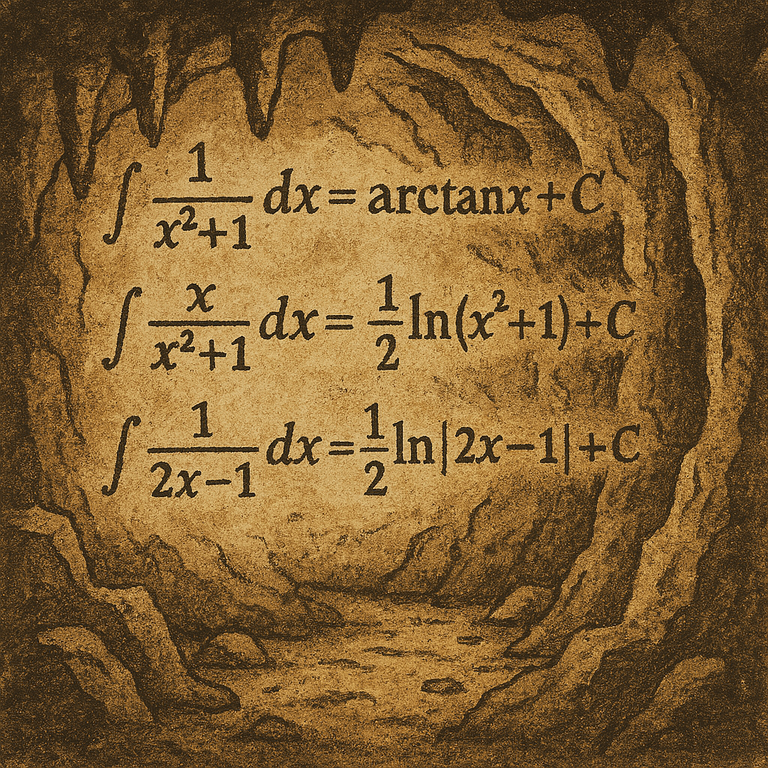
image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
Let's start with a warning, the integration of rational functions can be a difficult topic to digest.
First of all, let's talk about rational function. A rational function is obtained as a ratio of two polynomials with real coefficients. Example below.
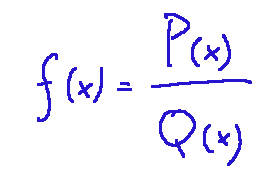
NOTE: a polynomial is an algebraic expression formed by a sum of monomial terms of the following type:
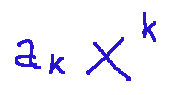
Where:
ak= coefficient belonging to a given numerical set
x = variable
k = a non-negative integer
The general form of a polynomial is as follows:
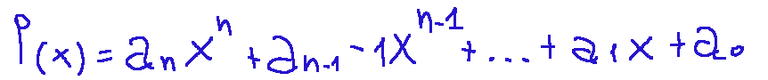
example
Here is an example of a polynomial of degree 4, principal coefficient 3, known term -5
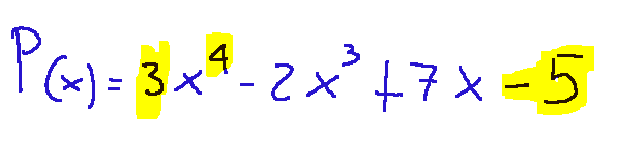
characteristics of a real function
-Domain D, i.e. all real numbers do not cancel the denominator
-As a function it has the characteristic of being continuous.
-Derivatives are rational
Here is the appearance of a rational function:
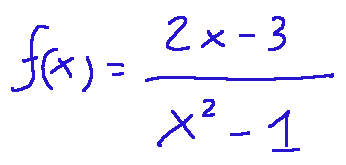
Integrations of rational functions
We have tried to transfer the concept of a rational function which in summary we can say is a ratio of polynomials.
The integral of a rational function is calculated with a procedure that is divided into three steps. These steps are called as follows:
-Division
-Decomposition into simple fractions
-Integration of each term
Exercise
If F(x) is the primitive of 2(2x2+x)/(2x-1) which is 3 in 1, then what is F(2)?
This exercise is certainly complicated, but I will try to show the steps to do it anyway.
Let's start from its description:
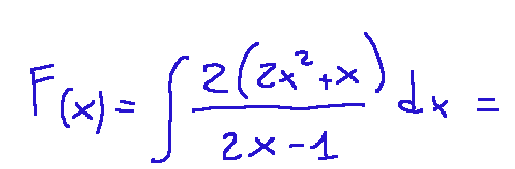
let's apply the first transformation
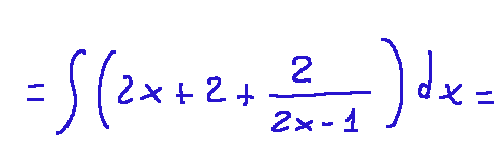
then we arrive at the form in which the constant is present C.
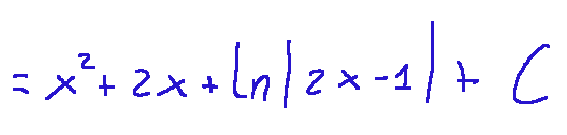
After a short reasoning we notice that F(1) = 3 gives the following condition:
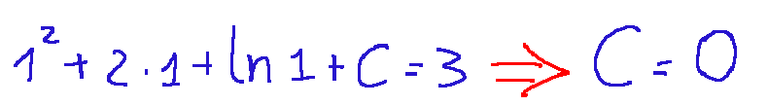
So we can write F(x)
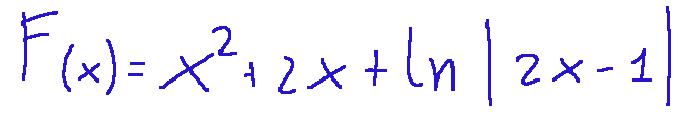
And now we calculate the function at x=2
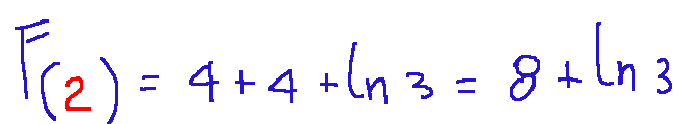
Result
the result is 8+ln3
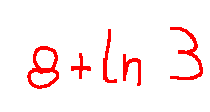
Conclusions
Integrating rational functions is useful in analytic geometry, physics, electrical engineering, and statistics.
Question
Did you know that Leonhard Euler, a Swiss mathematician and astronomer (also known as Euler) provided the practical tools for integrating rational functions that students use every day today?

ITALIAN

11-07-2025 - Analisi Matematica - Integrali di funzioni razionali [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-60-59)
Integrali di funzioni razionali
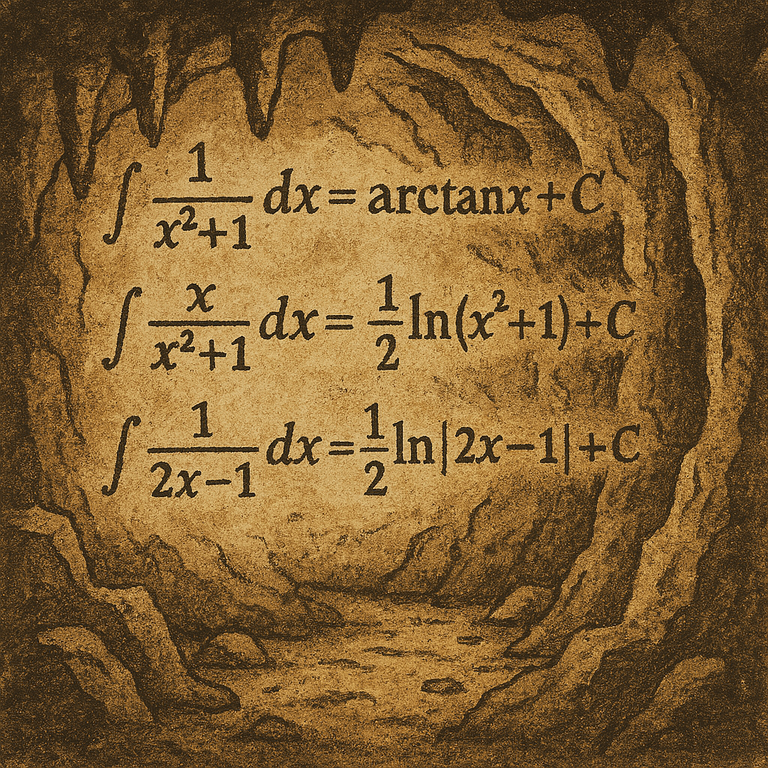
immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Partiamo subito con un avviso, l'integrazione di funzioni razionali può essere un argomento difficile da digerire.
Innanzitutto parliamo di funzione razionale. Una funzione razionale è ottenuta come rapporto di due polinomi a coefficienti reali. Esempio qui sotto.
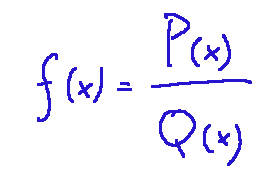
NOTA: un polinomio è un’espressione algebrica formata da una somma di termini monomî del tipo seguente:
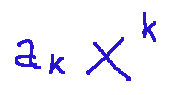
Dove:
ak= coefficiente appartenente a un dato insieme numerico
x = variabile
k = un numero intero non negativo
La forma generale di un polinomio è la seguente:
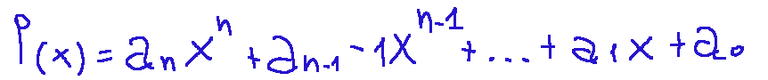
esempio
Qui di seguito l'esempio di un polinomio di grado 4, coefficiente principale 3, termine noto -5
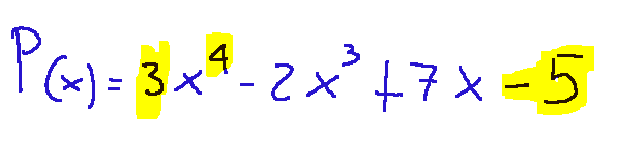
caratteristiche di una funzione reale
-Dominio D, cioè tutti i numeri reali non annullano il denominatore
-Come funzione ha la caratteristica di essere continua.
-Le derivate risultano razionali
Qui di seguito l'aspetto di una funzione razionale:
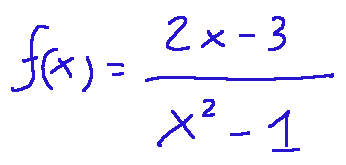
Integrazioni di funzioni razionali
Abbiamo cercato di trasferire il concetto di una funzione razionale che in sintesi possiamo dire che è un rapporto di polinomi.
L'integrale di una funzione razionale si calcola con un procedimento che è diviso in tre passi. Questi passi sono chiamati come segue:
-Divisione
-Decomposizione in fratti semplici
-Integrazione di ogni termine
Esercizio
Se F(x) è la primitiva di 2(2x2+x)/(2x-1) che vale 3 in 1, allora F(2) quanto vale?
Questo esercizio è sicuramente complicato, ma provo comunque a mostrare i passi per svolgerlo.
Partiamo dalla sue descriizione:
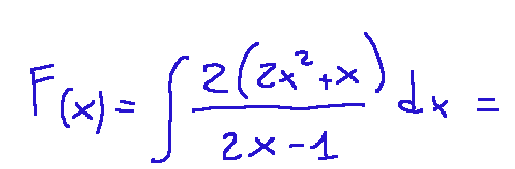
applichiamo la prima trasformazione
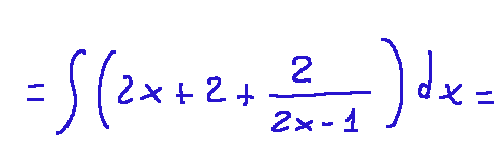
poi arriviamo alla forma in cui è presente la costante C.
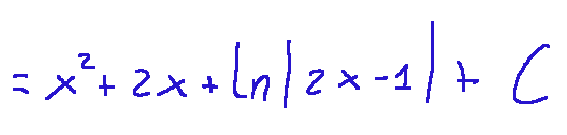
Dopo un breve ragionamento notiamo che F(1) = 3 fornisce la seguente condizione:
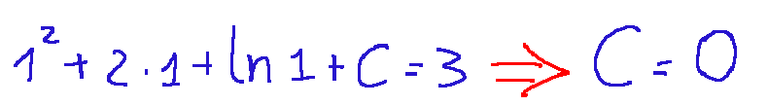
Quindi possiamo scrivere F(x)
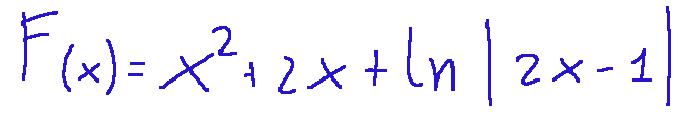
Ed ora calcoliamo la funzione in x=2
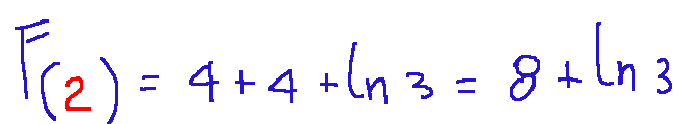
Risultato
il risultato è 8+ln3
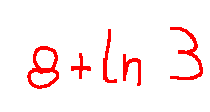
Conclusioni
L’integrazione di funzioni razionali è utile nell'ambito della geometria analitica, in fisica, in elettrotecnica e nella statistica.
Domanda
Lo sapevate che Leonhard Euler, matematico e astronomo svizzero (conosciuto anche come Eulero) fornì gli strumenti pratici per integrare le funzioni razionali che gli studenti usano oggi quotidianamente?
THE END
Congratulations @stefano.massari! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 84000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPPolinomi e monomi, altro ricordo sbloccato... Questo esercizio effettivamente non era proprio banale, ora da solo senza la tua guida non sarei riuscito a farlo 🤣
!PIZZA
Coi polinomi ricordo di aver fatto fatica... in realtà non sono complessi, ma la parola mi incuteva timore...hahah e forse mi irrigidivo durante la spiegazione e non la comprendevo. La spiegazione più semplice è dire che un polinomio è una somma di monomi. E qui se uno non sa che cosa è un monomio è fregato. Comunque un monomi è un termino di questo tipo:
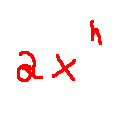
Dove:
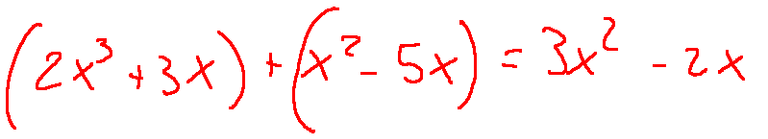
a = coefficiente
x = variabile
n = esponente intero non negativo
Un operazione di base con un polinomio può essere la seguente:
!WINE
Si il monomio era facile alla fine della fiera 🤣
!PIZZA
$PIZZA slices delivered:
@davideownzall(5/15) tipped @stefano.massari (x2)
Come get MOONed!
!discovery 30
Grazie Liberty per il tuo prezioso sostegno. Ogni mese faccio sempre dei passi in avanti con HIVE. Grazie soprattutto al tuo supporto. Ho passato i 20.000 HP qualche settimana fa e adesso sono molto contento di come stanno andando le cose. Quando avevo iniziato a fare questa tipologia di contenuti tecnici pensavo che prima o poi avrei dovuto smettere, invece, grazie soprattutto al tuo supporto riesco a continuare a farli e ad avere delle soddisfazioni. !BEER
View or trade
BEER.Hey @libertycrypto27, here is a little bit of
BEERfrom @stefano.massari for you. Enjoy it!Learn how to earn FREE BEER each day by staking your
BEER.View or trade
BEER.Hey @libertycrypto27, here is a little bit of
BEERfrom @stefano.massari for you. Enjoy it!Learn how to earn FREE BEER each day by staking your
BEER.This post was shared and voted inside the discord by the curators team of discovery-it
Join our Community and follow our Curation Trail
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program
This is entirely new to me
It’s an amazing topic anyway
Nice one!
Integrating rational functions is, in my opinion, a complex topic. It all starts with understanding how to write the integral, which I've included below. The integral is represented almost everywhere with an elongated letter s, which describes the interval of integration; in the example below, it's written in blue. After the integral, the function to be integrated is described; in the example below, it's written in red. Finally, we need to describe where we add the slices of infinitesimal width, and in this case, we do so on the x-axis (in the example below, the term representing this is written in black).
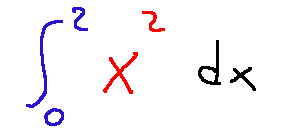
!CTP
Thank you so much for taking quality time of yours to actually explain this in deep. I really appreciate
Thank you for your kind words. To fully understand these concepts, it's essential to have a good understanding of integrals. For example, let's try to calculate a simple integral. Let's calculate the integral of x^2 in the interval from 0 to 2, which mathematically is written as follows:
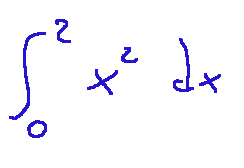
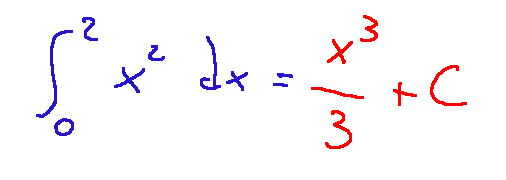
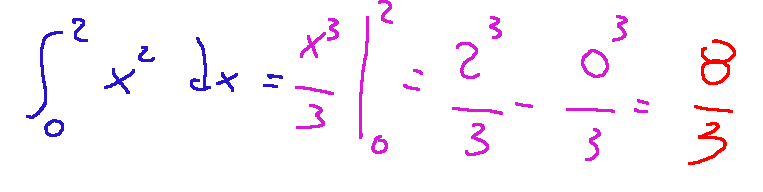
Now we find the primitive which is the following
and we apply the fundamental theorem of calculus
The numerical result is 8/3
!BBH
Very good calculation
In this article I also talked about primitives. In mathematical analysis, finding the primitive of a function means determining what we should derive to obtain that function. Below is an example where f(x) is on the left, and F(x) is on the right.
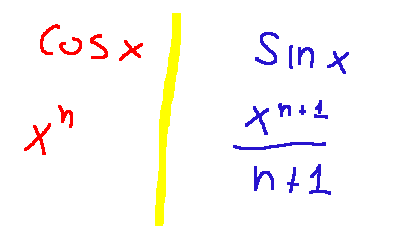
!ALIVE
great, in My school i learned as SinX / CosX = TanX
Yeah!!!! What you're talking about is precisely the fundamental trigonometric identity. I've reproduced the formula below in its mathematical notation—at least, in Italy we write it exactly as I do below.
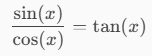
!LUV
Si potrebbe dire che quest'uomo, è ancora attuale poiché gli studenti mettono in pratica ciò che ha lasciato come eredità.
Leonhard Euler, che in Italia conosciamo come Eulero, ha dato contributi fondamentali in matematica, fisica, ingegneria, astronomia. Non so se ricordi, ma di lui esistono anche oggi tante cose in matematica che portano il suo nome:
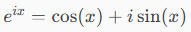
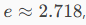
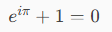
La formula di Eulero
Il numero di Eulero (che oggi è la base dei logaritmi naturali)
e una delle formule che alcuni matematici ritengono tra le più belle mai scritte, la formula Identità di Eulero:
!DIY
@stefano.massari, I paid out 0.166 HIVE and 0.035 HBD to reward 10 comments in this discussion thread.