09-07-2025 - Mathematical Analysis - Primitive and derivative [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH

09-07-2025 - Mathematical Analysis - Primitive and derivative [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-62)

Primitive and derivative

image created with artificial intelligence, the software used is Microsoft Copilot

The primitive
In mathematical analysis the primitive of a function f defined on an interval in which each element of I belongs to the real numbers is a function

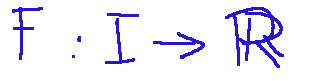
that satisfies the following relation for every x that belongs to the interval I

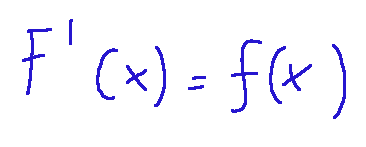
We can say that by deriving F we get exactly f.

Derivative and primitive
Two names that we have often heard in mathematical analysis. The derivative measures how a function varies at a point, while the primitive is the inverse operation of the derivative. Given a function f, the primitive is a function F such that F'=f

Now let's try to explain graphically what a derivative is and what a primitive is.

Derivative and its graph

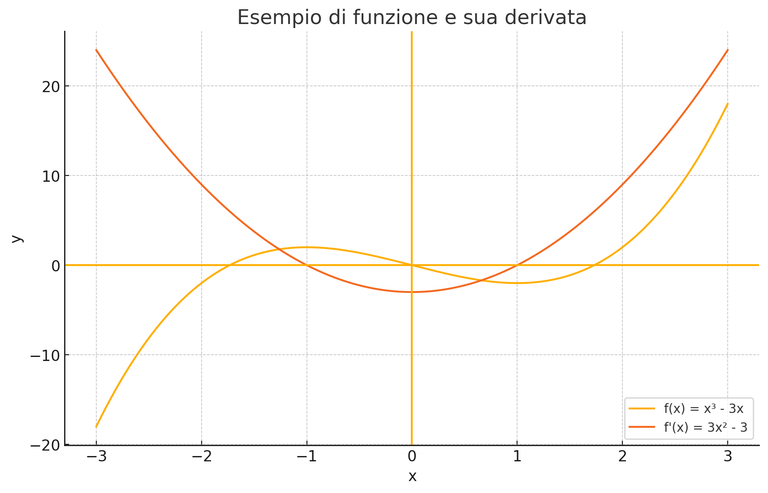
image created with artificial intelligence, the software used is ChatGPT

In this graph we have two functions, (1) is the starting function and (2) is its derivative
(1)

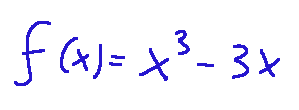
(2)

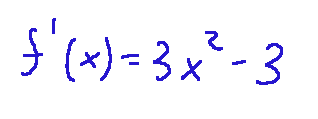
The yellow curve (1) is the starting function, while the red curve (2) is the curve that expresses the derivative of the function (1), that is, it is the instantaneous slope of f at each point.

Primitive and its graph
Here is a graph showing an example of a function and its primitive

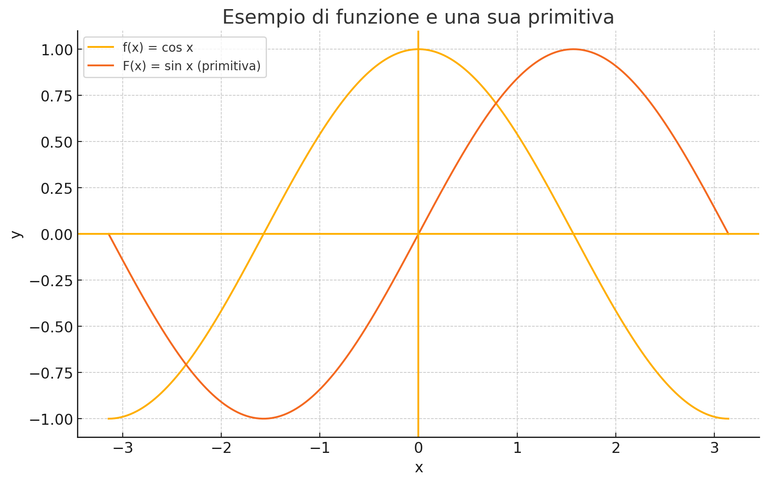
In the graph we have a yellow line (1) and an orange one (2).
The yellow line (1) represents the function:

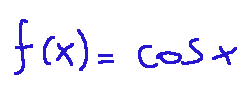
The orange line (2) represents the function:

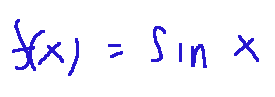
Looking at the graph we notice that at every point of the yellow curve, the initial one, the slope of the orange curve coincides and this shows the close connection between the function and its primitive.

In other words
The primitive of a function has as a difference from the source function an additive constant, that is, the source function and its derivative have identical curvature and the same maximum and minimum points.
We can say that a primitive is the same function shifted by a constant quantity.

Conclusions
In mathematical analysis, the study of functions is performed. In this study, we can obtain primitives and derivatives. The primitives of a function help us to calculate areas and volumes more easily, while derivatives help us to calculate the variation of a function.

Question
Did you know that the concept of derivative was developed by two great scientists, Newton and Leibniz, independently and almost simultaneously?

THE END

---

---

ITALIAN

09-07-2025 - Analisi Matematica - Primitiva e derivata [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-62)

Primitiva e derivata

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

La primitiva
In analisi matematica la primitiva di una funzione f definita su un intervallo in cui ogni elemento di I appartiene ai numeri reali è una funzione

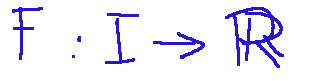
che soddisfa la seguente relazione per ogni x che appartiene all'intervallo I

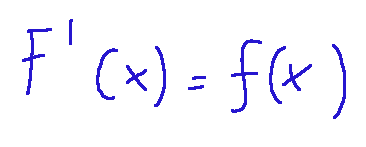
Possiamo dire che derivando F si ottiene esattamente f.

Derivata e primitiva
Due nomi che in analisi matematica abbiamo sentito spesso. La derivata misura come varia una funzione in un punto, mentre la primitiva è l'operazione inversa della derivata. Data una funzione f, la primitiva è una funzione F tale che F'=f

Ora proviamo a spiegare graficamente cosa è una derivata e cosa è una primitiva.

Derivata ed il suo grafico

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT

In questo grafico abbiamo due funzioni, la (1) è la funzione di partenza e la (2) è la sua derivata
(1)

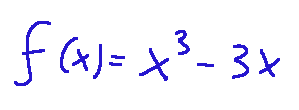
(2)

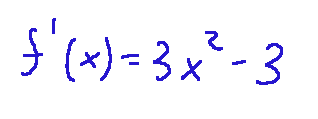
La curva (1) gialla è la funzione di partenza, mentre la curva (2) rossa è la curva che esprime la derivata della funzione (1), cioè è la pendenza istantanea di f in ogni punto.

Primitiva ed il suo grafico
Qui di seguito un grafico che riporta l'esempio di una funzione e la sua primitiva

Nel grafico abbiamo una linea gialla (1) e una arancione (2).
La linea gialla (1) rappresenta la funzione:

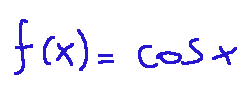
La linea arancione (2) rappresenta la funzione:

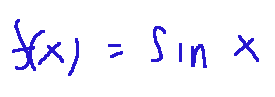
Guardando il grafico notiamo che in ogni punto della curva gialla, quella iniziale, l'inclinazione della curva arancione coincide e questo mostra il legame stretto che c'è tra la funzione e la sua primitiva.

In altre parole
La primitiva di una funzione ha come differenza dalla funzione di origine una costante additiva, cioè la funzione sorgente e la sua derivata hanno identica curvatura e stessi punti di massimo e di minimo.
Possiamo dire che una primitiva è la stessa funzione spostata di una quantità costante.

Conclusioni
In analisi matematica viene eseguito lo studio delle funzioni. In questo studio possiamo ottenere delle primitive e delle derivate. Le primitive di una funzione ci aiutano a calcolare più facilmente aree e volumi, mentre le derivate ci aiutano a calcolare la variazione di una funzione.

Domanda
Lo sapevate che il concetto di derivata fu sviluppato da due grandi scienziati, Newton e Leibniz, in maniera indipendente e quasi simultaneamente?

THE END