05-09-2025 - Operations Research - Systems of Linear Equations [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH

05-09-2025 - Operations Research - Systems of Linear Equations [EN]-[IT]
With this post, I would like to provide a brief introduction to the topic in question.
(lesson/article code: QE_05)

Image created with artificial intelligence, the software used is Microsoft Copilot

Introduction
Let's remember what operations research is. It is an educational subject that deals with optimizing a linear objective function subject to constraints.
Linear programming is a branch of operations research and is specifically concerned with maximizing or minimizing an objective function, which has constraints that are linear equations or inequalities.
Therefore, linear programming is closely linked to systems of linear equations because these form the constraints.
Below is the formalism of a linear system showing an inequality:

The close connection between linear programming and linear equations

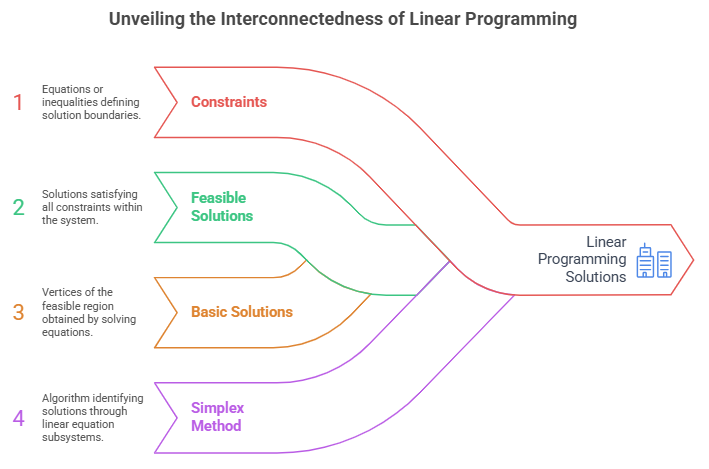
Image created with artificial intelligence, the software Napkin.ai is used.

Constraints
In linear programming, constraints are equations or inequalities.
Feasible Solutions
A system of linear equations defines a set of solutions.
Basic Solutions
In linear programming, basic solutions
Basic solutions are points obtained by choosing m basic variables and setting the others to zero. Technically, they represent the vertices of the feasible region, but this is a difficult concept to understand if you've never performed a linear programming exercise. These points are found by solving sets of linear equations.
Simplex Method
The simplex method is perhaps the most popular algorithm in linear programming. In this method, the solutions of subsystems are identified; subsystems are composed of linear equations.

System of Linear Equations
Example 01
A system of linear equations is shown below.

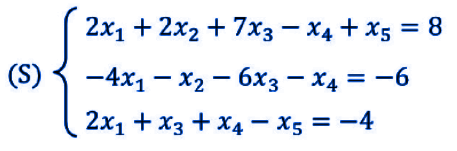
In this system, we have 5 variables: x1, x2, x3, x4, x5.
The system of equations finds a solution with the following values ​​of the variables: x1=0, x2=2, x3=0, x4=4, x5=8.
Performing the various substitutions, we obtain the following:

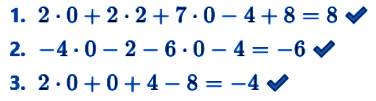
Example 02
Now let's analyze the following system of linear equations:

From the second equation, we know that 2x2=4, so x2=2
But if we now solve the third equation, we'll find that if x1+x2=8, then x1=6

However, we'll discover that by substituting x1 and x2 into the first equation, we'll get that

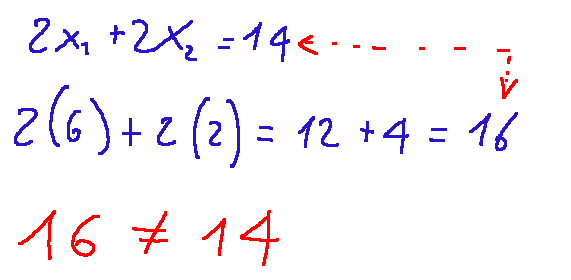
Which means that this system has no solutions.
If a linear programming problem had these constraints, we might immediately conclude that there are no solutions, and therefore we can immediately understand that the problem we're tackling, perhaps a logistics or cost-cutting problem, has no solution under the given constraints. Essentially, we would save a lot of time and avoid wasting time trying to optimize a system that cannot be optimized.

Conclusions
We can conclude by saying that linear programming is entirely built on systems of linear equations. The constraints of various linear programming problems are linear systems with equalities or inequalities. By solving these systems, we find the optimal points. What does this mean? This means that by solving linear programming problems, we can maximize a company's profit, minimize the cost of a product, or minimize the length of a transportation route.

Question
Did you know that airlines have used and still use linear programming? Airline problems are very complex. Did you know that flight schedule planning has countless constraints and variables, and is therefore analyzed using linear programming and systems of equations? (Like the ones shown, but much more complex)

ITALIAN

05-09-2025 - Ricerca operativa - Sistemi di equazioni lineari [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(codice lezione/articolo: QE_05)

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Introduzione
Ricordiamo cosa è la ricerca operativa. Essa è una materia d'istruzione che si occupa di ottimizzare una funzione obiettivo lineare soggetta vincoli.
La programmazione lineare è una branca della ricerca operativa ed è proprio quella che si occupa di massimizzare o minimizzare una funzione obiettivo, la quale presenta dei vincoli che sono equazioni o disequazioni lineari.
Quindi la programmazione lineare è fortemente legata ai sistemi di equazioni lineari perché questi formano i vincoli.
Qui di seguito riporto il formalismo di un sistema lineare dove è mostrata una diseguaglianza:

Lo stretto legame tra la programmazione lineare e le equazioni lineari

immagine creata con l’intelligenza artificiale, il software usato è Napkin.ai

I vincoli
In programmazione lineare i vincoli sono equazioni o disuguaglianze
Le soluzioni ammissibili
Un sistema di equazioni lineari definisce un insieme di soluzioni
Soluzioni di base
In programmazione lineare le soluzioni di base
Le soluzioni di base sono punti ottenuti scegliendo m variabili di base e ponendo le altre a zero. Tecnicamente rappresentano i vertici della regione ammissibile, ma questo è un concetto difficile da comprendere se non si è mai eseguito un esercizio di programmazione lineare. Questi punti si trovano proprio risolvendo insiemi di equazioni lineari.
Metodo del Simplesso
Il metodo del simplesso è forse l'algoritmo più popolare della programmazione lineare. In questo metodo vengono identificate le soluzioni dei sottosistemi, i sottosistemi sono composti da equazioni lineari.

Sistema di equazioni lineari
Esempio 01
Qui di seguito è mostrato un sistema di equazioni lineari

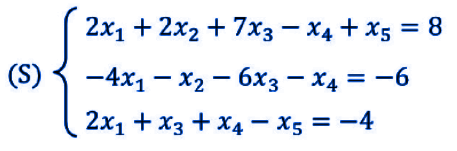
In questo sistema abbiamo 5 variabili che sono: x1,x2,x3,x4,x5.
Il sistema di equazioni trova soluzione con i seguenti valori delle variabili: x1=0,x2=2,x3=0,x4=4,x5=8.
Eseguendo le varie sostituzioni otteniamo quanto segue:

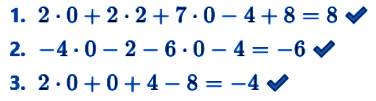
Esempio 02
Ora analizziamo il seguente sistema di equazioni lineari

Dalla seconda equazione sappiamo che 2x2=4, quindi x2=2
Ma se ora andassimo a risolvere la terza equazione avremo che se x1+x2=8, per forza di cose x1=6

Scopriremmo però, che andando a sostituire x1 e x2 nella prima equazione avremo che

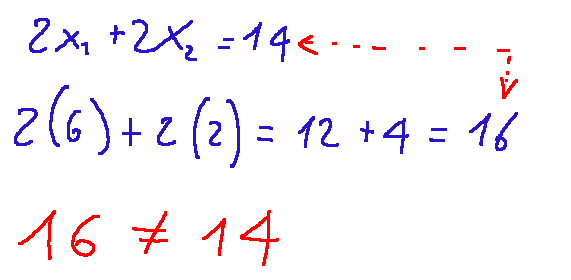
Il che significa che questo sistema non ammette soluzioni.
Se un problema di programmazione lineare avesse questi vincoli, potremmo subito arrivare alla conclusione che non ci sono soluzioni e quindi possiamo subito capire che il problema che stiamo affrontando, magari un problema di logistica o di riduzione costi, con i vincoli dati, non ha soluzione. Sostanzialmente risparmieremmo un sacco di tempo e non andremmo ad eseguire tentativi inutili per ottimizzare un sistema che non si può ottimizzare.

Conclusioni
Possiamo concludere dicendo che la programmazione lineare è costruita tutta su sistemi di equazioni lineari. I vincoli dei vari problemi di programmazione lineare sono sistemi lineari con uguaglianze o disuguaglianze. Risolvendo questi sistemi si trovano i punti ottimali. Cosa significa questo? Questo significa che risolvendo dei problemi di programmazione lineare possiamo massimizzare il profitto di un azienda, minimizzare i costi di un prodotto o il tragitto di un trasporto.

Domanda
Lo sapevate che le compagnie aeree hanno utilizzato ed usano tuttora la programmazione lineare? I problemi delle compagnie aeree sono problemi molto complessi, lo sapevate che la pianificazione degli orari di volo ha tantissimi vincoli e tantissime variabili e per questo viene analizzata tramite programmazione lineare e sistemi di equazioni? (tipo quelli mostrati, ma molto più complessi)

THE END